余剰電力により重量物を上部に持ち上げて位置エネルギーとして保存しておき、電力が必要になったときそれを落下させて電力を得る装置を考えます。これはいわば屋内でできる揚水発電であって、原理は極めて単純であり構造も簡単となります。実用化には程遠いのですが、将来のためにその理論および技術を今から蓄積しておく必要があると思います。
1. 背景および構想

電気を蓄えるには、現在そのほとんどを蓄電池に頼っていますが、これは化学反応を利用してエネルギーを蓄える方法です。もちろんその効率と利便性には優れているのですが、何度も使うと劣化して使用には限界があります。一方、揚水発電は重力を利用するのみで、原理的には再生可能な蓄電装置といえます。この原理を応用して、水の代わりに重りを使用し、その装置を建物内あるいは地下に設置すれば、廃棄物の出ないクリーンなエネルギー貯蔵装置となります。この構想を実現化するには、面積のとらない重力蓄電装置を一つのユニットとし、それらを束ねてプラント化すれば可能となります。
この設備を設計するにあたって、それぞれのユニットの充電放電効率が重要になります。とくに、放電部分は重力を用いて発電するので、この重力発電のエネルギー変換の力学的メカニズムを知っておく必要があります。
2. 重力蓄電装置の構造
重量物(重り)をワイヤーを介して、一定の高さに設置したプーリーに固定します。このプーリーはギアボックス(増速機)を経由して、そのシャフトを発電機に接続しておきます。この発電機は電動機と兼用として、外部からの電力によって回転させて下部の重りを持ち上げるように設計します(図1)。ギア比が大きければ、小さな回転力(トルク)でかなり大きな重量をつり上げることが可能です。上部に移動した重りは、加えられた電力を位置エネルギーの形で蓄えます。それを落下させると、開放されたエネルギーは発電機を回し、再び電力に変換されます。この落下は自由落下ではなく、ほぼ等速運動となります。この落下速度は発電機に与える回転数を決め、出力電力に関わってきます。
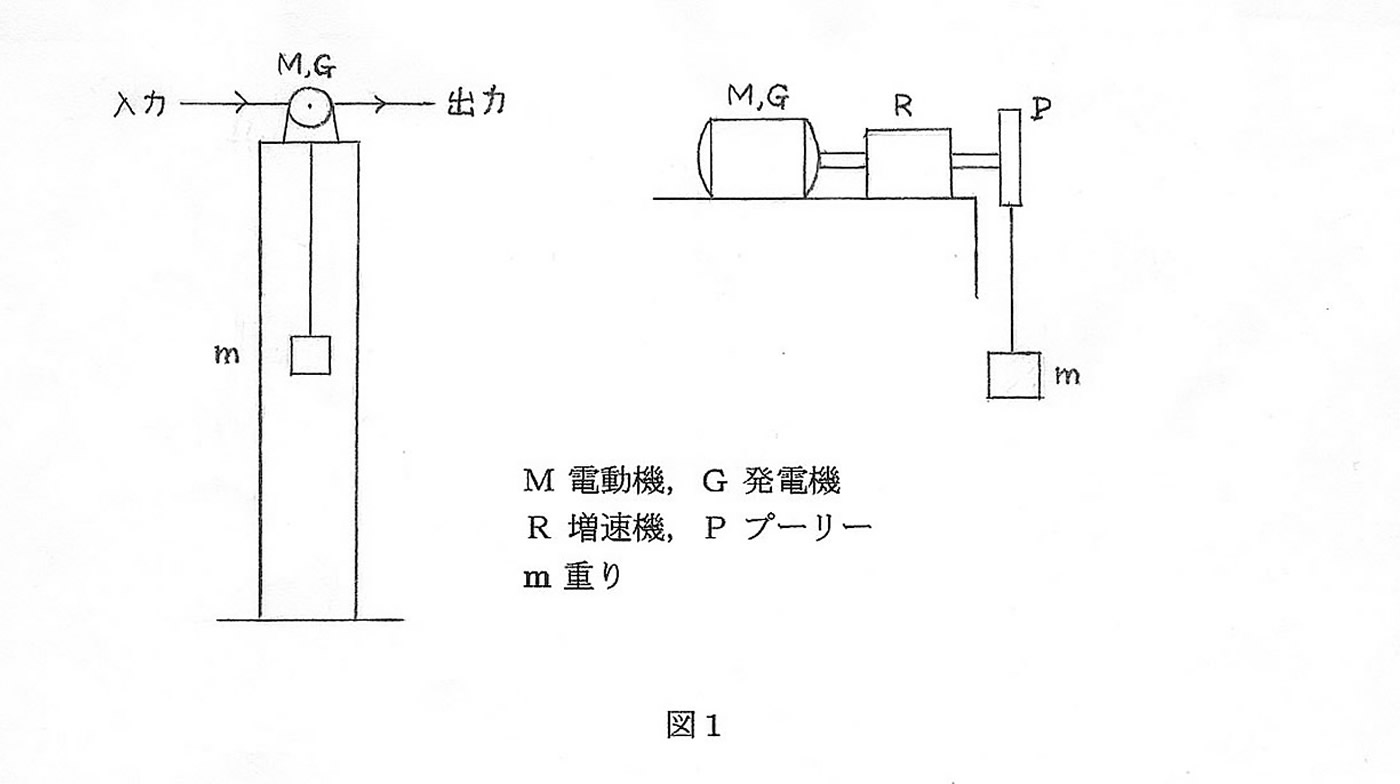
使用する重りは密度の高いもの、例えば鉛を用います。重りを滑らかに落下させるためには、ガイドが必要となります。上部に回転を制御するブレーキやギア変速機を備えれば十分です。重りの重量が大きくなれば、それらを支持する構造体の強度にも注意する必要があります。
3. 重力発電の力学
重力蓄電装置において、出力部分すなわち重力発電の効率は全体の蓄電効率に深く関わってきます。その発電効率を上げるには、このエネルギー変換の力学的かつ電気的な考察が必要となってきます。
重力によって落下する物体が、運動方向と逆にその速度に比例する抵抗力を受けて落下するとき、その物体はそのうちほぼ一定の速度で落下します。これは力のバランスによるものです。重力 m の物体を初め速度 0 の静止状態から落下させたとき、t 時刻後の落下速度 v は
\[ \tag{1} v = \frac{mg}{K}(1 - e ^{-\frac{K}{m}t}) \]で表せます。ここで、g は重力加速度で、K は抵抗力についての比例定数です。重力発電の場合、この定数 K は発電機や増速機のギア摩擦などによる機械的負荷を表します。式(1)により、じゅうぶん時間が経った後の速度 v はほとんど mg/K となることが分かります(図2)。
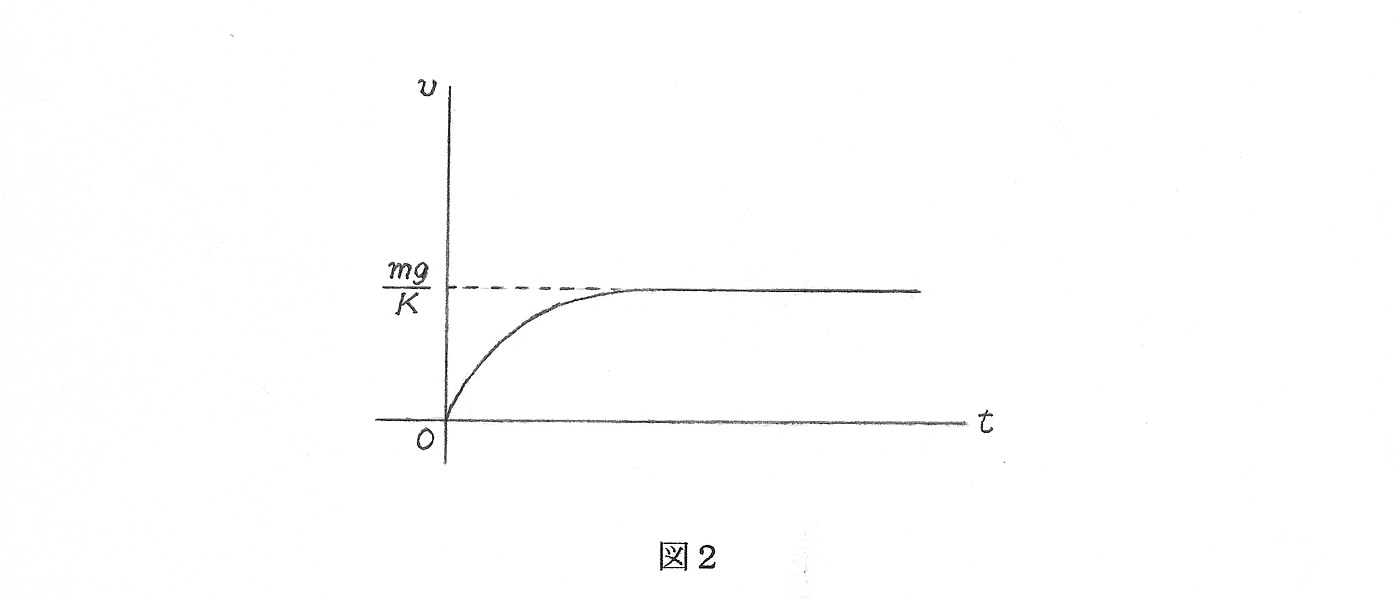
式(1)を基にして、これよりエネルギー変換に関するいろいろな量を計算することが可能になります。例えば、出力評価や落下運動の持続時間、発電効率などの理論値が分かります。これにより、外部から制御できる変数(パラメーター)の主な役割を知ることができます。高さを固定したとき、増速機のギア比 k と重りの重量 m、プーリーの直径 d の3つのパラメーターが重要となります。とくに、k は概ね落下の持続時間をきめ、重量m は出力を、また d は発電機にかかるトルクに大きな影響を与えます。発電機の種類にもよりますが、出力は発電機に与えられた回転数の外にトルクにも依存します。したがって、よい出力を得るには、これら3つの要素のバランスが大切になってきます。
4. 実験結果
この理論を検証するために、実際に装置を組み立てて、発電部分すなわち重力発電の実験をしてみます。この特性を知ることは、さらに大きな規模の装置を設計するためにも必要なことになります。実験に使用した装置は小規模のものですが、理論だけでは予想もつかないいろいろな事実も確認できます。そこで得られたデータの一部を紹介します。
実験に使用した発電機は、自己励磁式の交流発電機で定格出力が 700W のものです。電圧調整のためにコンデンサーが付いていました。出力電力を調べるには、発電機の外部回路に負荷(抵抗)をかけて、その回路に流れる電流 I とそのときの発電機の起電力 E を測定します。発電機の内部抵抗はほとんど 0 に近いので、外部抵抗の両端に現れる電圧 V を測定して、その起電力としました。すると、出力電力 P は P = E1 = VI より計算できます。また、落下時間(持続時間)to を測定すれば、エネルギー変換率がつぎのように求められます。重量 m の重りを高さ l まで持ち上げたとき、蓄えられる位置エネルギー U は U = mgl で表されます。これを t0 時間かけて落下させたとき、放出される電気的エネルギー(電力量)は Pt0 だから、このときのエネルギー変換率 c は
\[ \tag{2} c = \frac{Pt_0}{U} = \frac{Pt_0}{mgl} \]で表されます。したがって、L = mgl - Pt0 は変換に伴うエネルギー損失を意味します。そこで、実験結果はつぎのようになります。
実験1. 増速機の倍率を 48 倍、すなわちギア比を k = 48 に設定します。重りの重量を m = 90(kg)に、またプーリーは直径 d = 13.3(cm)のものを用います。この重りを高さ l = 130(cm)まで持ち上げて落下させます。外部抵抗が R = 10(Ω)のとき、外部回路には電流が I = 3.24(A)で電圧が V = 32.6(V)の出力が得られました。このとき発電機は P = 105.6(W)の電力を生成したことになります。落下時間は to = 5.8(秒)でしたので、式(2)により、エネルギー変換率は c = 53.4(%)と計算されます。さらに、電流の最高値は外部抵抗が R = 5(Ω)のとき I = 4.3(A)となり、電圧の最高値は回路が開放状態のときで V = 153.0(V)を記録しました。電流・電圧特性は、外部にかけた負荷抵抗の値によって変わります(図3)。
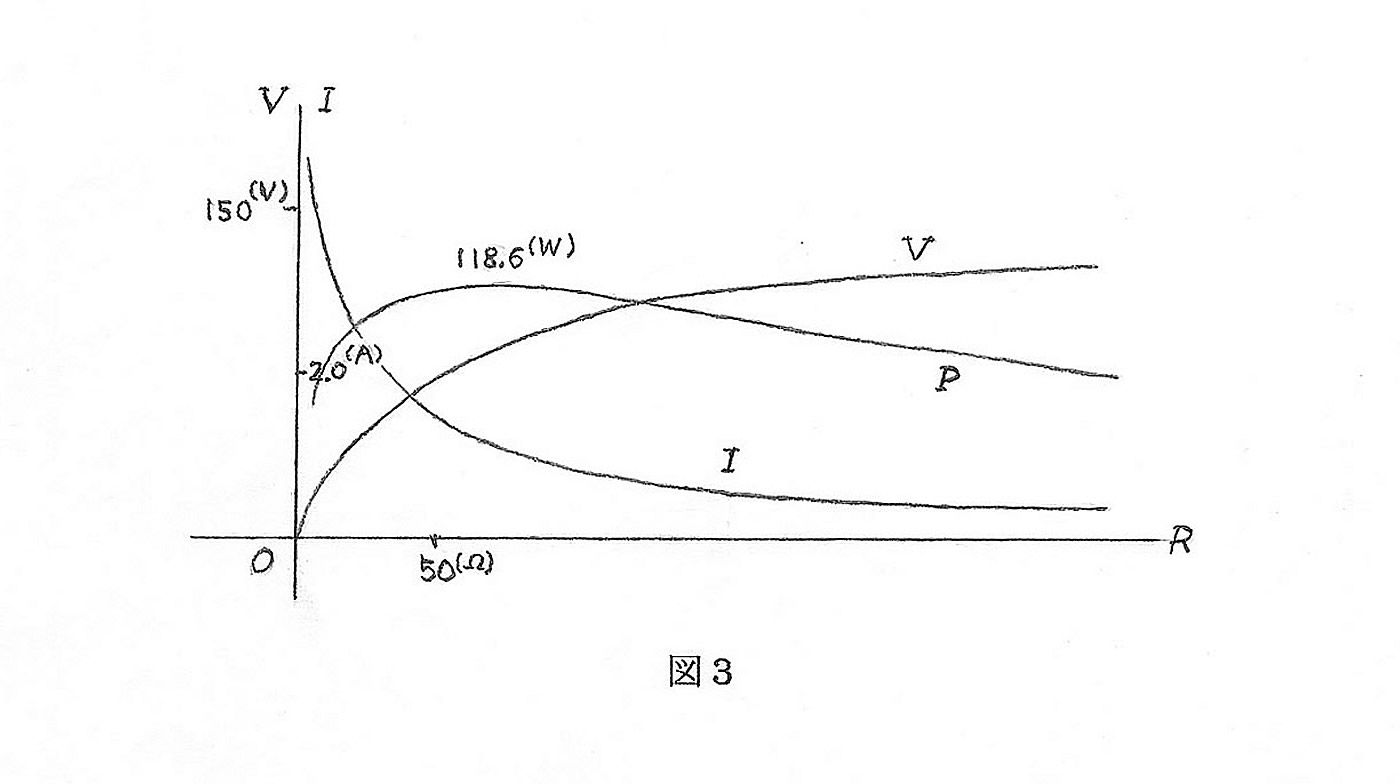
実験2. ギア比を k = 100にして、重量を m = 106(kg)、プーリーの径 d = 15.3(cm)で同様の実験を試みました。結果は以下の通りです。外部抵抗が R = 10(Ω)のとき、電流は I = 1.98(A)で電圧が V = 24.9(V)でした。したがって、出力電力は P = 49.3(W)となります。落下時間は t0 = 9.6(秒)でしたので、エネルギー変換率は c = 35.0(%)になります。実験1と比較して出力が落ちた原因は、ギア比 k を倍増したためで、これにより落下時間が2倍に延びています。これはエネルギー保存則より当然のことといえます。一般に、運転の持続時間が延びれば、瞬間出力は減少します。
5. 今後の方針
以上の結果を踏まえて、仮想の試算をしてみます。地上で考えられる装置の可能な規模は、最大で高さ l = 100(m)、重量が m = 10(ton)程度だと思われます。プーリーの径 d とギア比は全体のバランスできめることにします。これによって蓄えられる位置エネルギーは U = mgl = 9.8 × 106(J)で、これをエネルギーの損失がないとして、30分かけて(秒速5.5(cm)で)落下させたときの瞬間出力は
\[ \tag{3} P = \frac{U}{t_0} = 9.8 \times 10^6 / 1800 = 5.44 (kW) \]となります。これはこの装置一基あたりの出力で、これを一つのユニットとして並べて建物内に格納します。一基の占める面積が小さいの、数100(m)四方の建物ならば、1万基を収納できます。すると、これで 5.44 × 104(kW)= 54.4(MW)の電力を溜めることが可能となります。放電の際に、ユニットをつぎつぎとリレー式に運転させれば、運転時間を延ばすことができます。また、いくつかを同時に作動させて、出力を調整することも可能です。
この試算は、充電および放電の途中で生ずるエネルギー損失を全く考えていません。実際の効率はかなり低いと思われますが、将来それが改善されて実用化できれば、その効用は大きなものになります。この蓄電方法は環境に対してクリーンで、しかも何度でも繰り返し使用でき、原理的には消耗するものは何もありません。現在基礎研究の段階ですが、今後解決しなければならない問題がたくさんあります。出力を大きくするには、設備の大型化が必要となります。また、全体の効率を上げるには、発電機その他の機械的ロスを低く抑えなければなりません。しかし、これは将来の技術力に委ねることになります。
この研究をさらに進めるには、個人の力に限界があります。そこで研究費の面で、また技術的な点で支援が必要となります。現在、この研究に対するスポンサーと技術に関するアドバイザーを求めています。
尚、この研究の詳細な内容については、いづれ出版によって公表するつもりです。
2018 年 3 月
追記
本稿の続編「重力蓄電装置の力学2(→)」を公開いたしました。ぜひ、ご一読下さい。
2019 年 1 月
本稿の続編「重力蓄電装置の力学3(→)」を公開いたしました。ぜひ、ご一読下さい。
2019 年 2 月