Consider a machinery getting the electric power from gravitational energy, stored as the potential energy making use of a surplus electric energy. It is the same way as a pumped storage power station, excepting with a wight in place of water. The mechanism is very simple, so the system may be settled in a building. This paper is a survey of the dynamical theory for the battery by gravity, together with some data.

1. Background

At the present day, we are usually relying on a chemical battery to store the electric energy. This battery is very easy and useful , but it becames useless after the many times charging. On the other hand, a pumped storage power station is a good system with respect to ecology. It is to say a renewable storage battery owing to gravity, provided with a dam. If it is made use of a weight instead of water, then there needs no dam.

To be realized the above conception, construct a tower having a weight and a generator, that is said an unit of the storage cell. Then, bundle up them and settle in a building. On the planning, an interesting thing is the efficiency for charging and discharging. Especially the part of discharging is the most important, because its output power is generated by gravitation. So we must know the dynamical mechanism concerning with the energy transformation for an unit.

2. Mechanical structure

Hang up a weght through a wire from a pulley, fixed on a higher position. The pulley is connected to the generator by the shaft, with a gear box for speed control. The generator may be used by way of a motor to lift up the weight, in this case it is worked by a surplus electric power from the outside (see Figure 1). As the ratio of the gear is higher, so the torque on pulley is larger, then the motor be able to lift up the more heavy weight.

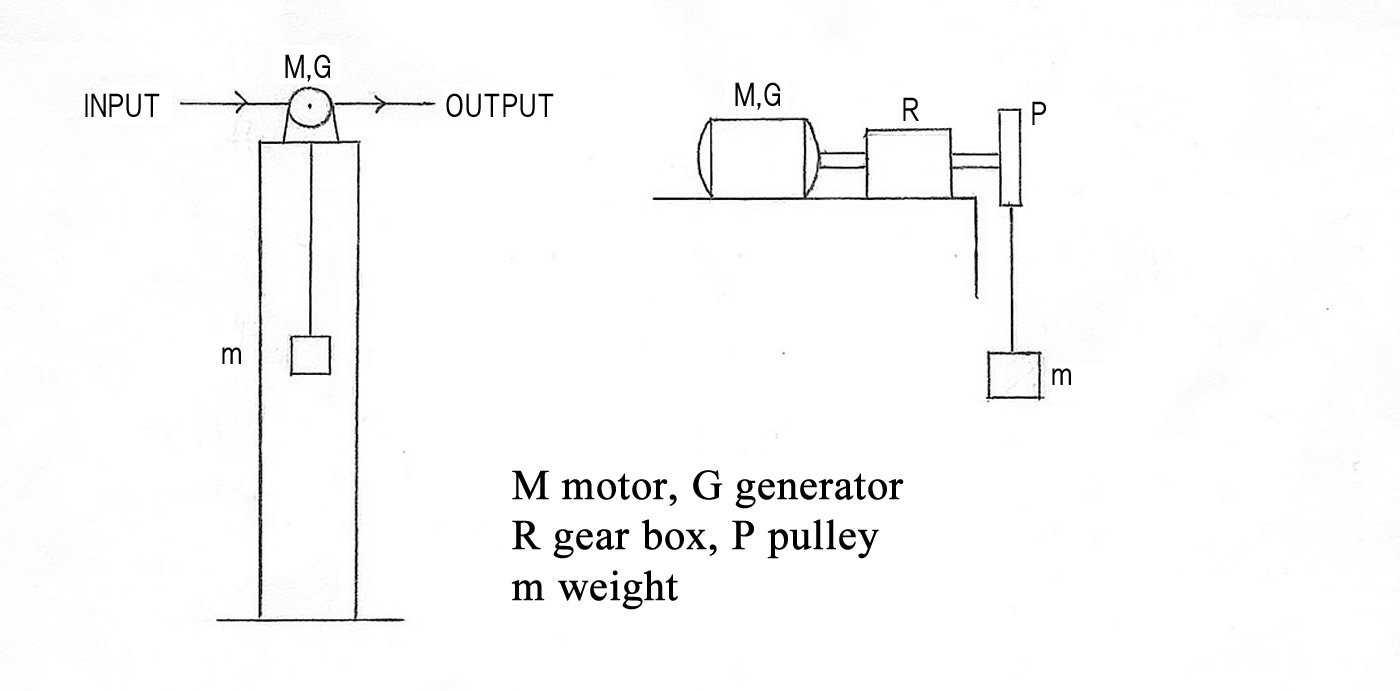
Figure 1

The weight in place of upside keeps a given electric energy in the form of potential energy. If the weight falls down, then it revolves the pulley and the generator, so that the electric energy arise again. The fall motion of the weight has a nealy constant speed, but not a free fall motion. The dropping speed of the weight decides the revolution of generator, and it is concerned with output power.

On the matter of the weight, it is good to have a large density such as a lead. In order to fall the weight smoothly, it may be required a guide. It is sufficient to provide a brake and a transmisson for the speed control, on upper space. Moreover, take care of the construction supporting the heavy weight.

3. Dynamics of gravity battery

In respect of the gravity battery, the efficiency by way of a battery is depends almost all on the output part. The output power is generated by gravitation, so it is interested and important to study about the generation by gravity. A dynamical problem is how to change effectively from the potential energy into the electric energy.

When a mass body falls down by gravity, if the magnitude of the resistance force is proportional to the dropping speed, then it falls with a constant speed eventually. This is a result by balance on the two forces. Suppose that the matter having mass m is fallen with the initial velocity 0. Then, the velocity v of the motion at a time t after, is expressed as follows.

\[ \tag{1} v = \frac{mg}{K}(1 - e ^{-\frac{K}{m}t}) \]

Here, g is the gravity acceleration and K is the proportional constant for the resistance force. In the case of the gravity battery, this constant K shows a mechanical load caused by firiction of the generator and the gear box. By equation (1), it is clear that the velocity v becomes to mg/K in practice, at the long times after (Figure 2).

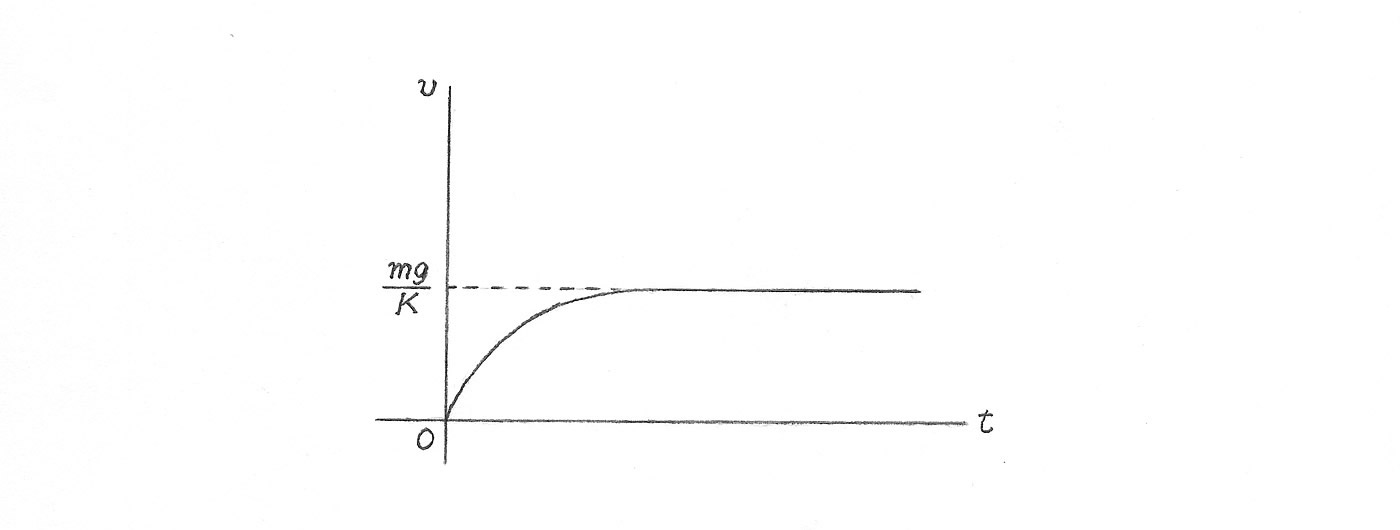
Figure 2

On the basis of the equation (1), a many quantities can be calculated with respect to the energy transformation. For instance, the time during the motion of weight, the revolution of generator and the estimate of output power, are derived from (1). Then, it is shown how to play the role of each parameter as a external variable. There are the important three parameters, the ratio k of gear unit, the mass m of the weight, and the diameter d of pulley. That is, k decides the time during the motion mainly, m decides the output power, and d have an effect on a torqu to the generator. The output power of generator depends not only on the revolution but on the torque. Therfore, a balance among these parameters is important on account of good output.

4.Experiment and the result

For verification of the theory, we make actually the experiment for the output power generated by gravitation. It is necessary to know such characteristic feature of the generation, in order to design a more large system. Our system used in the experiment is small scale, but many various facts are found, these are not expected by the theory. We explain below the results with a peace of data getting by the experiment.

The generator used in the experiment is an alternating generator having a self exciter with the formal power 700 W. It possesses a condenser for voltage regulation. In order to measure the output power, set a resistance on the external circuit and take measure of the current I together with the electromotive force E of the generator. Since the internal resistance of the generator is nearly 0, the voltage V arisen on the external resistance may be regarded as the electromotive force. Then, the output power P is derived from P = EI = VI.

By measurement a time t₀ during the motion of weight, the ratio of the energy transformation is able to know as follows. Consider the weight with mass m settled on a place of height l, then the weight has a potential energy U denoted by U = mgl. When the weight falls taking the time t₀, the electric energy Pt₀ is released out for that time. Then the ratio c of the energy transformation is derived from the following equation.

\[ \tag{2} c = \frac{Pt_0}{U} = \frac{Pt_0}{mgl} \]

Therefore, L = mgl – Pt₀ means the energy loss in the energy change. Thus, the results of experiment are described in the following way.

Case 1. We set up the ratio k of the gear box into 48 times, that is k = 48. The mass of weight is m = 90 (kg), and the diameter of pulley is d = 13.3 (cm). Let fall the weight from the height l = 130 (cm). Then, for the external resistance R = 10 (Ω), we get the current I = 3.24 (A) and the voltage V = 32.6 (V) on the external circuit. In this case, the generator created the electric power P = 105.6 (W). Since the time of motion is t₀ = 5.8 (s), we find the ratio of energy transformation c = 53.4 (%) by (2). The maximum of current shows I = 4.3 (A) for the resistance R = 5 (Ω), and the maximum of voltage V = 153.0 (V) on the open external circuit. The characteristic pictures of current and voltage have severally a different feature, for the value of resistance (Figure 3).

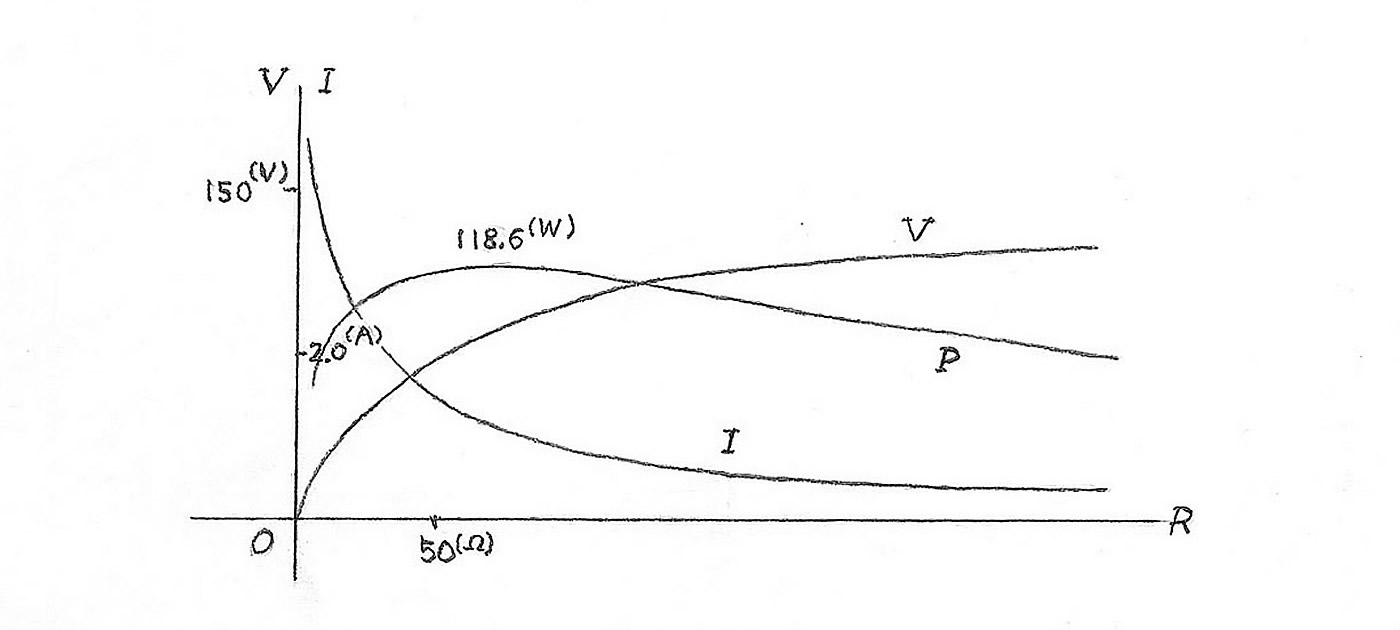
Figure 3

Case 2. We set the ratio of gear be k = 100, the mass of weight be m = 106 (kg), and the diameter of pulley be d = 15.3 (cm). The result is following way. For the external resistance R = 10 (Ω), it shows the current I = 1.98 (A) and the voltage V = 24.9 (V). Therefore, the output power is P = 49.3 (W) in this case. As the time of motion is t₀ = 9.6 (s), the ratio of energy transformation is derived as c = 35.0 (%) from (2). In comparison with the Case 1, the output power goes down and while the time of motion becomes to double long time, these are caused by the larger ratio of gear. In general, the output power is so small as a time of motion to be long. It is just due to the energy conservation law.

5. Planning in future

We make a imaginary calculation, based on the above result. A system, in scale as large as possible on a ground, may be made with the maximal height l = 100 (m) and the mass of weight m = 10 (ton). The diameter d of pulley and the ratio k of gear are decided by a balance on the whole. Then, the apparatus stores the potential energy U = mgl = 9.8 × 10⁶ (J). When the weight falls with the motion dureing the time 30 minutes (the velocity is 5.5 cm per second), the output power is expected as following

\[ \tag{3} P = \frac{U}{t_0} = 9.8 \times 10^6 / 1800 = 5.44 （kW） \]

without the energy loss.

This output power is the power for one unit. Settle many machines as for the unit in a building. Since the floor area of an unit is small, it may be equiped with ten thousand units, in the area of some hundred metres square. Then, this plant is able to store the electric power 5.44 × 10⁴ (kW) = 54.4 (MW). In discharging, if the unit is maked to work one after the other, then the running time is able to be long. Furthermore, if some of the units are maked working simultaneously, we can have a power control.

The above estimate is not under consideration for the energy loss arised on charge and discharge process. It seems that the practical efficiency is small by far. However, if this system becomes a reality for the future, then the effectiveness is very large. This storage method is clean for environment and it is possible to use repeatedly. In principal, it has no waste matter.

For the present, the study of this method remains at a fundamental step and there are many problems which must be settled from now on. In order to get a large output power, it needs a large sized equipment. Besides it must be diminish the mechanical loss to make a good efficiency. But these problems are left for the advancement of technology in future.

December 2018