これは、本文「重力蓄電装置の力学的考察(→)」の続編です。装置その他の概要は、「本文」を参照して下さい。用語や記号もそれに従います。
重力による蓄電装置の充電部分は、外部からの電力によって重りを上に吊り上げるだけなので、その力学的機構はよく知られていることです。問題はその放電部分であって、これは重りに蓄えられた位置エネルギーをその落下によって電気エネルギーに変換させるところです。この重力による発電の部分で要求されることは、以下の2つが考えられます。
- ① 出力を大きくすること。
- ② 運転時間(落下時間)を長くすること。
この①は蓄電効率に関係し、②は装置の実用性から必要なことです。しかし、装置の規模が同じとき、出力と運転時間は反比例の関係にあります。そこに、力学的な考察が必要となる理由があるのです。
1. 落下速度
重りの質量を \(m\) として、これを高さ \(l\) の位置から落下させたときの、重りの運動を考えます。重りはワイヤーで上部に置かれたプーリーに繋がれ、そのシャフトが増速機(ギア)を経由して発電機を回す仕組みになっています。装置の上端を原点 \(x = 0\) として、下方に \(x\) 軸をとります。いま、重りを上端から初速度 \(0\) で離したとき、重りはいろいろな抵抗を受けながら落下していきます。その主な要因は、発電機から受ける機械的な抗力と増速機のギアによる摩擦力が考えられます。これらはその回転数に、したがって落下速度 \(v\) に比例すると仮定します。すると、重りの運動はいずれ等速度運動となることがつぎのようにして分かります。
重りは下方に重力 \(mg\) を、また上方に抵抗力 \(f = Kv\) を受けるので、合わせて \(F = mg - Kv\) の力が下方に働きます。一方、力 \(F\) は加速度 \(a = dv/dt\) を生じさせます。これらの間には「ニュートンの法則」によって、\(F = ma\) の関係があるので、これは \(v\) に関する微分方程式となります。とくに \(t = 0\) で \(v = 0\) となる解 \(v\) は、次式のようになります。
\[ \tag{1} v = \frac{mg}{K}(1 - e ^{-\frac{K}{m}t}) \]これが重りの時刻 \(t\) における速度 \(v\) を表します。この式で \(t\) を十分大きくすると、\(v\) は \(mg/K\) に近づき、重りは速度 \(mg/K\) の等速度運動となることが分かります。また、この速度が高さ \(l\) に関係しないことも注意すべきところです。
時刻 \(t_0\) における重りの位置 \(x\) は \(v = dx/dt\) を積分して、(1)式から求められます。結果はつぎのようになります。
\[ \tag{2} x = \frac{mg}{K}\begin{pmatrix}t - \frac{m}{K}(1 - e ^{-\frac{K}{m}t})\end{pmatrix} \]これより、重りの落下時間(下面に達するまでの時間)\(t_0\) は、(2)式で \(x = l\) とした時刻 \(t_0\) としてきまります。すなわち、\(t_0\) は
\[ \tag{3} t_0 = \frac{m}{K}\begin{pmatrix}1 - e ^{-\frac{K}{m}t_0}\end{pmatrix} + \frac{Kl}{mg} \]を満たします。この \(t_0\) を一つの式として表すのは難しいのですが、式の形から、\(K\) が大きいときは \(t_0\) も大きくなることが分かります。
定数 \(K\) は抵抗力の比例定数であって、この \(K\) の値は重要となりますので「負荷定数」と呼ぶことにします。この値は発電機の容量や増速機のギア比によります。さらに、外部抵抗の値にも依存します。それは、外部回路に流れる電流が大きいほど、発電機にも大きな負荷がかかり回転数が下がります。このとき、\(K\) の値は大きくなります。外部から \(K\) の値を測定することは無理ですが、\(t_0\) を測定することにより、(3)式から \(K\) をきめることは可能です。
2. 出力評価
この蓄電装置による出力エネルギーの評価をしてみます。初めに高さ \(l\) の重りに蓄えられたポテンシャルエネルギー(位置エネルギー)は \(E = mgl\) で、\(t\) 時刻後には「エネルギー保存則」から、つぎのように各エネルギーに分配されます。
\[ \tag{4} E = T + U + W \]ここで、\(T\) は \(t\) 時刻における重りのもつ運動エネルギーで、\(U\) はそのときのポテンシャルエネルギー、\(W\) は発電機が \(t\) 時刻までにした仕事を表します。途中でのエネルギー損失は考えていません。
これらはつぎのように計算されます。運動エネルギー \(T\) は、(1)式により、
\[ \tag{5} T = \frac{1}{2}mv^2 = \frac{m^3g^2}{2K^2}\begin{pmatrix}1 - e ^{-\frac{K}{m}t}\end{pmatrix}^2 \]となります。この関数 \(T = T(t)\) は \(t\) に関して単調増加で、大きな \(t\) で一定値 \(m^3g^2/2K^2\) に近づきます。また、式(2)によって、\(U\) は
\[ \tag{6} U =mg(l-x)= mgl - \frac{m^2g^2}{K}t + \frac{m^3g^2}{K^2}\begin{pmatrix}1 - e^{-\frac{K}{m}t}\end{pmatrix} \]が得られます。この \(U = U(t)\) は単調減少で、\(t\) が増加すると殆んど直線 \(U = mgl + m^3g^2/K^2 - (m^2g^2/K)t\) に近づき、\(t = t_0\) で \(U = 0\) となります(図1)。
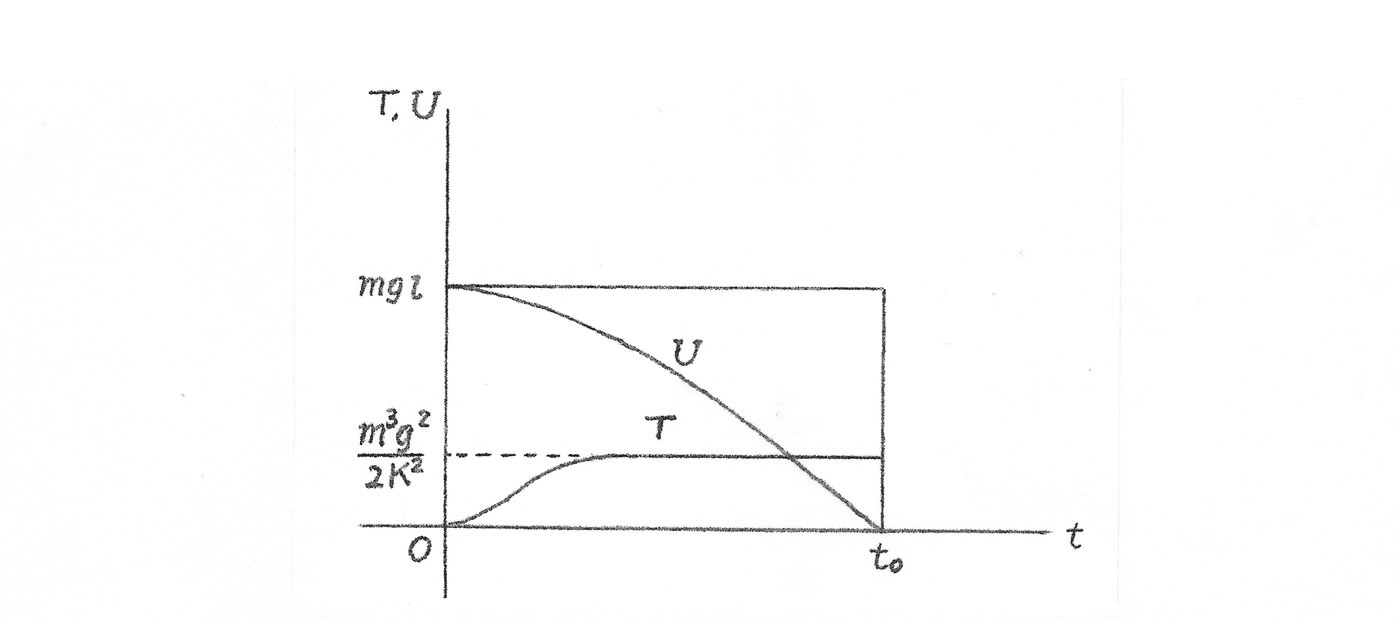
ギア摩擦などの散逸力を考慮しなければ、抗力 \(f = Kv\) は発電機が受ける負荷と考えられます。したがって、重りが \(x\) の位置に来るまでに発電機がした仕事 \(W\) は、仕事の定義と \(v = dx/dt\) より、
\[ W = \int^x_0 fdx= K\int^x_0vdx = K\int^t_0v^2dt \]とかけます。式(1)を用いて、これを求めると
\[ \tag{7} W = \frac{m^2g^2}{K}t - \frac{m^3g^2}{K^2}\begin{pmatrix}1 - e^{-\frac{K}{m}t}\end{pmatrix} - \frac{m^3g^2}{2K^2}\begin{pmatrix}1 - e^{-\frac{K}{m}t}\end{pmatrix}^2 \]が得られます。もちろん、式(4)から \(W = mgl - T - U\) として、これに式(5)と式(6)を代入しても同じ結果となります。この曲線は、大きな \(t\) に対して殆んど直線
\[ W = \frac{m^2g^2}{K}t - \frac{3m^3g^2}{2K^2} \]に近くなります(図2(a))。
各エネルギー \(T\)、\(U\) 、\(W\) のグラフを縦方向に重ねると、式(4)により \(E = mgl\)(一定)となります(図2(b))。これは、初めのエネルギー \(mgl\) が \(t\) 時刻後にそれぞれのエネルギー \(T\)、\(U\)、\(W\) に分配されていく様子を表しています。
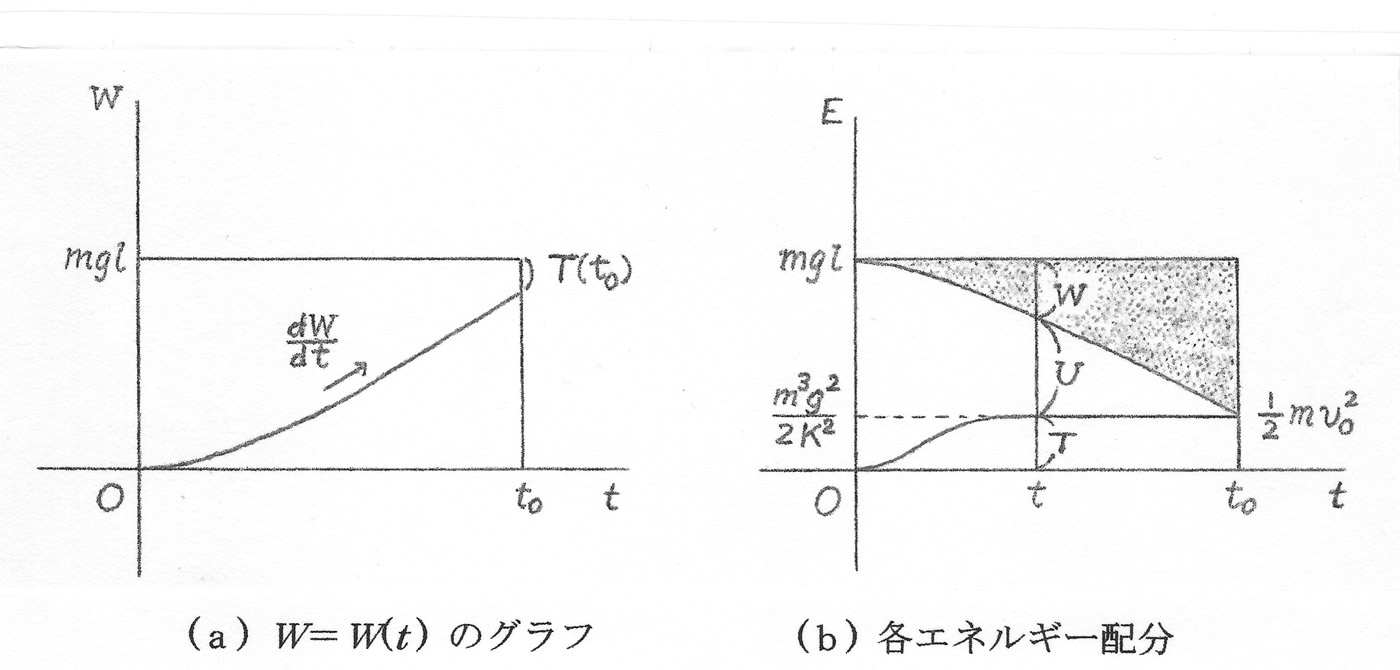
この図で、上部の影を付けた部分が発電機のした仕事となります。最終時刻 \(t_0\) において運動エネルギー \(T_0 = (1/2)mv_0^2\) の残余が生じます。ここで \(v_0\) は、(1)式と(3)式によって、\(v_0 = g(t_0 - Kl/(mg))\)とかけます。したがって、これを小さくするのが望ましいのですが、全く \(0\) にすることはできません。
抗力 \(f\) のする仕事率 \(P\) は、式(7)から直ちに求められ、
\[ \tag{8} P = \frac{dW}{dt} = \frac{m^2g^2}{K}\begin{pmatrix}1 - e^{-\frac{K}{m}t}\end{pmatrix}^2 \]となります。これは曲線 \(W = W(t)\) の勾配であり、大きな \(t\) で一定値 \(m^2g^2/K\) に近づきます(図2(a))。この仕事率 \(P\) が時刻 \(t\) における発電機が生成する電力と考えられます。すると、発電機の最終的な総出力は
\[ \tag{9} W_0 = \int^{t_0}_0 \frac{dW}{dt}dt = W\begin{pmatrix}t_0\end{pmatrix} = mgl -\frac{mg^2}{2}\begin{pmatrix}t_0 - \frac{Kl}{mg}\end{pmatrix}^2 \]となります。
結局、発電効率を上げるには、\(K\) と \(t_0\) を大きくして \(v_0\) を小さく抑えるのがよいと思われます。実際には、増速機のギア比を大きくして発電機の回転数を上げ、重りをゆっくり落とせばよいのです。しかし、これを実行するには難しいところがあります。
3. 運転持続時間
これは落下時間 \(t_0\) のことで、この時間が長いほど実用的にはよいわけです。この \(t_0\) をきめる主な要素を調べるためには、(3)式を解けばよいのですが、これが簡単ではありません。そこで、つぎのように近似をします。負荷定数 \(K\) が重量 \(m\) に比べて大きいときは、\(K/m \gt 1\) なので \({e^{-(K/m)t}}_0 \ll 1\) とみなし、(3)式から、持続時間 \(t_0\) を
\[ \tag{10} t_0 = \frac{m}{K} + \frac{Kl}{mg} \]としてよいでしょう。実際の実験上でも \(K \gt m\) となるのは確認されています。
式(3)の形から、\(t_0\) は比率 \(\lambda = K/m\) のみできまります。すなわち、(3)式は
\[ \tag{11} e^{-λt_0 } = -λt_0 + 1 + \frac{l}{g}λ^2 \quad\begin{pmatrix}λ = \frac{K}{m}\end{pmatrix} \]とかき直せます。そこで、この解を \(t_0 = t_0(λ)\) とかき、\(dt_0/dλ\)を求めると
\[ \tag{12} \frac{dt_0}{dλ} = -\frac{t^2_0-(l/g)λ_0-(2l/g)}{λ(t_0-(l/g)λ)} = - \frac{t_0}{λ} + \frac{2l}{g} \cdot \frac{1}{λ(t_0-(l/g)λ)} \]となります。いま、\(m\) を固定して \(K\) をパラメーターとみると、\(t_0 = t_0(λ)\) は \(K\)、したがって \(λ\) についての増加関数となるはずです。すなわち \(dt_0/dλ \gt 0\) であって、(12)式によれば \(t_0 - (l/g)λ \gt 0\)、\(t_0^2 - (l/g)λt_0 - (2l/g)\lt 0\) でなければなりません。これより、\(t_0\) の存在範囲として
\[ \tag{13} \frac{l}{g}λ \lt t_0 \lt \frac{l}{2g}\begin{pmatrix}λ+\sqrt{λ^2 + \large{\frac{8g}{l}}}\end{pmatrix} \]が得られます。これによって、持続時間 \(t_0\) のおおよその大きさが分かります。
式(13)より、\(\lambda\) または \(l\) が大きいときは、殆んど \(t_0 = (l/g)λ = Kl/(mg)\) としてよいと考えられます。例えば、\(m = 1\)(ton)、\(l =10\)(m)、\(K = 10^6\) としたとき、\(λ = 10^3\) で \(t_0 = 1020\)(s)を得ます。このときの仕事率は \(P_0 = 96.04\)(W)で、総出力は \(W_0 = 9.8 × 10^4\)(J)となります。これは、残余の運動エネルギー \(T_0\) が殆んど \(0\) に近く、初めに与えたポテンシャルエネルギーがそのまま発電にまわされていると考えられます。
4. 結論
運転時間 \(t_0\) を延ばすには(10)式より \(K\) を大きくすればよく、そのために外部から制御できる量として、増速機のギア比を大きくする必要があります。これは同時に、落下速度を小さくして残余の運動エネルギー \(T_0\) を小さく抑える効果も生みます。この \(T_0\) が大きいとエネルギーの無駄だけでなく、床面に大きな衝撃を与え、場合によっては事故のもとにもなります。
しかし、ただ単にギア比だけを上げてもよい結果は得られません。大きい出力を考えるならば、発電機に与える回転数と同時に、一定以上の回転力(トルク)が必要なように思われます。そのためには、プーリーの径を大きくして同時に重りの重量を増やす必要があります。これらのバランスは、理論で考えるほど単純ではありません。別の観点からみれば、この現象の複雑さが興味を引くところです。
2019 年 1 月
追記
本稿の続編「重力蓄電装置の力学3(→)」を公開いたしました。ぜひ、ご一読下さい。
2019 年 2 月