1. まえがき
地球上どこでも磁石で方位を測ると、その針の N 極はつねに北の方角を指します。これは地球が磁場を持っているためで、地球を磁石に喩えると北極が S 極で南極が N 極の大きな磁石になっていると考えられます。したがって、地表での磁力線は南極から出発して北極に至る方向となります。この地球の磁場は「地磁気」と云われ、宇宙から地球を電子的に守るシールドになっています。
ところが、この地磁気の方向が地球の歴史上何度も反転してきたといわれています。最近の反転は過去 77 万年前に起こって現在の状態になったそうです。この痕跡が千葉県養老川沿いの地層に記録されています(チバニアン)。現在のところ、この「地磁気逆転」のメカニズムについて、はっきりと解明されていないようです。(上の写真は、千葉県養老川の風景写真です)
電磁気学の結果によると、電流すなわち電荷の移動によって磁場が生成されます。もし 地球内部の電荷を持つ流体が、その運動により電流を発生させ、それが磁場を生成すると考えれば地磁気の存在を説明することはできます(ダイナモ理論)。ただし、これだけでは 逆転の現象は説明できません。
そこで、全く別の機構で上のものと逆向きの磁場が生成されれば、二つの磁場の強弱によって地磁気逆転の可能性について説明ができると考えられます。そのための力学モデルを、以下に説明します。
2. 地球の内部構造
地球は、半径 \(R=6370\)(km)の球体と考えられ、表面と中心部が固体の他はそのほとんどが半固体の流動性物質(マグマ)で出来ていると考えられています。 詳しくは、半径を 100 として、1/100 が地殻、44/100 がマントル、55/100 が核の3層から成っていて、とくに中心部 19/100 は内核といわれ、密度の高い固体で固められています。その外側 36/100(外核)は金属性の物質による液体層で、この流体運動が地磁気を発生させていると考えられています。
地球の体積の大部分を占めるマントルは半固体の物質から成り、内部では熱対流(マグマ)が起こっていて、これがプレート運動を引き起こすと考えられています。
3. 自転による磁場
地球を電荷を持った球体と考え、それが 1 日で 360° の角速度で回転しているものとすれば、その電荷の回転によって生ずる電流により磁場が発生します。この磁場が地磁気にどの程度の影響を及ぼすかを調べてみます。そのために、電磁気学からのつぎの結果を利用します(証明は付録を参照して下さい)。
補題 1. 半径 \(R\) で一様な電荷密度 \(\rho\) をもち、角速度 \(\omega\) で回転している球体(中心 O)の内部の点 P の磁場は \[ \tag{1} \mathbf{B}(\mathbf{r}) = \frac{\mu_0 \rho (5R^2 - 3r^2)}{15}\boldsymbol{\omega} \quad (0\leq r \leq R) \] とかける。ただし \( \overrightarrow{\mathrm{OP}} = \mathbf{r}\) (\(|\mathbf{r}| = r \)) で、\( \mu_0 \) は真空の透磁率である。
地球の回転軸と、地磁気の N 極と S 極を結んだ線はほぼ一致していると考えられているので、地球内部の自転による磁場のつくる磁力線の方向は、南極から北極へ貫く直線となります(地磁気の軸)。しかし、これでは地表での磁力線の向きが実際のものと逆になってしまいます。そこで、外核に存在する流体の回転運動による磁場が、自転による磁場と逆向きになるように回転方向を仮定します。
4. 外核の流体がつくる磁場
外核の中を動く流体の回転運動を、地軸(地磁気の軸)に直交する平面上で地球の中心を回る円電流と考えて近似します。電流の方向は地球の自転と逆向きで、その大きさを \(I\) とします。このとき、軸上の各点での磁場の強さは、つぎの補題から分かります(証明は付録を参照して下さい)。
補題 2. 定常電流 \(I\) が流れている半径 \(R_0\) の円電流を考える。この中心から垂直距離 \(z\) における磁場の大きさは \[ \tag{2} B(z) = \frac{\mu_0 I}{2} \frac{R_0^2}{(R_0^2+z^2)^{3/2}} \] できまる。
地軸上の磁場の大きさと方向は、上で導入した二つの磁場を重ねることによって得られます。とくに、自転による磁場の方向は軸上で南極から北極方向へ、また外核流体による磁場は北極から南極へ向かいます。結果として、軸上では二つの磁場は相殺され、あるいは向きの決定が不安定となります。
5. バランス条件
自転による磁場 \(\mathbf{B}_1\) と、外核流体によって生ずる磁場 \(\mathbf{B}_2\) の大きさを比較してみます。それらは軸上で互いに向きが逆なので、それらが合成された磁場が 0 となる条件(バランス条件)を調べてみます。
そこで、北極点における磁場のバランス条件を考えます。(1)式で \(r = R\)(地球の半径)とおき、(2)式で \(z = R\) として \(B_1 = B_2\) の関係をつくると \[ \tag{3} \frac{\mu_0\rho(2R^2)\omega_1}{15} = \frac{\mu_0I}{2}\frac{R_0^2}{(R_0^2+R^2)^{3/2}} \] となります。ここで \(\omega_1\) は地球の自転の角速度を表します。\(d=R_0/R\) とおいて(3)式を単純化すると、次式が得られます。 \[ \tag{4} I = \frac{4}{15} \frac{1+d^2}{d^2} R^3\rho\omega_1 \]

図 1
地球と共に自転する、体積電荷密度 \(\rho\) による電荷の総量を \(Q_1\) とすると、\( Q_1 = (4/3) \pi R^3 \rho \) とかけます。一方、外核の円電流として流れる電荷量を \(Q_2\) とし、これが角速度 \(\omega_2\) で軸のまわりを回っていると仮定します。すると、線電流の電荷密度 \( \lambda = Q_2/(2 \pi R_0) \) を用いて、\(I=\lambda\upsilon\) とかけます。 ここで \( \upsilon \) は電荷の移動速度で、この場合 \(\upsilon = R_o\omega_2 \) です。結局、\( I = Q_2\omega_2/(2\pi)\) となり、バランス条件(4)式は \[ \tag{5} Q_2\omega_2 = \frac{2}{5} \frac{1+d^2}{d^2} Q_1\omega_1 \] とかけます。外核の位置を考えて、\(d = R_0/R\) は大体 \(1/3\) あたりになります。
6. 評価
バランス条件(5)は、\(d=1/3\) のとき \( Q_2\omega_2 = 4Q_1\omega_1 \)となります。あるいは、 \[ \tag{6} \omega_2 = 4 \frac{Q_1}{Q_2} \omega_1 \quad (=\omega_0) \] とかいてみます。実際に、数値の上で条件(5)または(6)が成り立つときがあるかは不明です。しかし、この可能性を仮定した上で、以下の状況を考えます。式(6)の右辺は、地球の要素として決まる不変量と考えて、これを \(\omega_0\) とおきます。すると、外核の中を移動する流体の角速度 \(\omega_2\) が大きい \(\omega_2 > \omega_0 \) 場合、(3)式では不等号(\( < \))が成り立ち、 \(B_1 < B_2 \) となることから北極点での磁場の方向は軸上で北極から南極の方を向いています。これは現在の地磁気の方向と一致します。一方、\(\omega_2\) が小さく \(\omega_2 < \omega_0 \) のときは、地磁気の向きは逆となります。
流体の角速度 \(\omega_2\) が、臨界値 \(\omega_0\) を越えるかそれ以下であるかによって磁場の方向が逆転するということは、この現象が力学的に大変不安定であることを示しています。すなわち、時間的尺度でいえば、地球の歴史の上でこの逆転現象が過去に何度も起きていたであろうことが推察されます。
付録
以下に、補題 1. 2. の証明を示します。
1. 補題 1 の式(1)の導出:ベクトルポテンシャル \( \mathbf{A} \) を用いれば、磁場は \(\mathbf{B} = \nabla \times \mathbf{A} \) とかけます。角速度ベクトル \( \boldsymbol{\omega} \) が、 \( z \) 軸方向となる \( xyz \) 座標系から、位置ベクトル \( \mathbf{r} \) が \( z' \) 軸上になるような新しい座標系 \( x'y'z' \) を設定します。このとき、ベクトル \( \boldsymbol{\omega} \) が \( x'z' \) 面にくるように \( x' \) 軸をきめ、 \( \boldsymbol{\omega} \) と \( z' \) 軸の間の角度を \( \psi \) とします。すると、ベクトルポテンシャル \( \mathbf{A} \) はつぎのようになります。
\[ \tag{7} \mathbf{A}(\mathbf{r}) = \frac{\mu_o}{4\pi} \int \frac{\mathbf{J}(\mathbf{r'})}{| \mathbf{r}-\mathbf{r'}|} d\tau' \] このとき \(\mathbf{J} = \rho \mathbf{v} ,\; \mathbf{v} = \boldsymbol{\omega} \times \mathbf{r'} \) であり、\(d\tau' = r'^2 \sin\theta'dr'd\theta'd\phi'\) とかけます。\( \boldsymbol{\omega} \) と \( \mathbf{r'} \) の成分を (\( r',\theta',\phi' \)) でかき、\( \mathbf{v} = \boldsymbol{\omega} \times \mathbf{r'} \) を計算するとつぎのようになります。 \[ \begin{align*} \mathbf{v} = \omega r' \big( &-(\cos\psi \sin\theta' \sin\phi') \mathbf{e}_{x'} \\ &+ (\cos\psi \sin\theta' \cos\phi' - \sin\psi \cos\theta') \mathbf{e}_{y'} \\ &+ (\sin\psi \sin\theta' \sin\phi') \mathbf{e}_{z'} \big) \end{align*} \]ここで、(\( \mathbf{e}_{x'},\mathbf{e}_{y'},\mathbf{e}_{z'} \))は座標系 \( x'y'z' \) の単位ベクトルを表します。すると、(7)式の \( \phi' \) についての積分をした結果はつぎの形になります。
\[ \tag{8} \mathbf{A} = \frac{-\mu_0\rho\omega\sin\psi}{2} \left(\int_0^R \int_0^\pi \frac{r'^3 \cos\theta' \sin\theta'}{\sqrt{r^2 + r'^2 - 2rr'\cos\theta'}} dr'd\theta' \right) \mathbf{e}_{y'} \]そこで、\( \theta' \)の積分を計算します。\( u=\cos\theta' \) とおいて、 \[ \begin{align*} I &= \int_0^\pi \frac{r'^3 \cos\theta' \sin\theta'}{\sqrt{r^2 + r'^2 - 2rr'\cos\theta'}}\, d\theta' = r'^3 \int_{-1}^1 \frac{u}{\sqrt{r^2 + r'^2 - 2rr'u}}\, du \end{align*} \] \[ = \begin{cases} \dfrac{2}{3}rr' & ( r' > r )\\ \dfrac{2r'^4}{3r^2} & ( r' < r ) \end{cases} \] となります。すると、(8)式の積分部分は \[ \int_0^R Idr' = \int_0^r Idr' + \int_r^R Idr' = \frac{5R^2 - 3r^2}{15} \quad (0 < r < R) \] さらに、\(\boldsymbol{\omega} \times \mathbf{r} = -\omega r \sin \psi \mathbf{e}_{y'}\) に注意すると、(8)式から \[ \tag{9} \mathbf{A}(\mathbf{r}) = \frac{-\mu_0\rho (5R^2 - 3r^2)}{30}(\boldsymbol{\omega} \times \mathbf{r}) \] ときまります。これより \(\mathbf{B} = \nabla \times \mathbf{A} \) をつくれば、(1)式が得られます。
2. 補題 2 の 式(2)の導出:対称性を利用して、ビオ・サバールの法則で垂直成分のみを考えればよい。よって、\( z \) 点での磁場の大きさは \[ B(z) = \frac{\mu_0}{4\pi}I \int \frac{ds}{r^2} \cos\theta = \frac{\mu_0 I}{4\pi} \frac{\cos\theta}{r^2} \int ds = \frac{\mu_0 I}{2} \frac{R_0^2}{(R_0^2 + z^2)^{3/2}} \] とかけます。
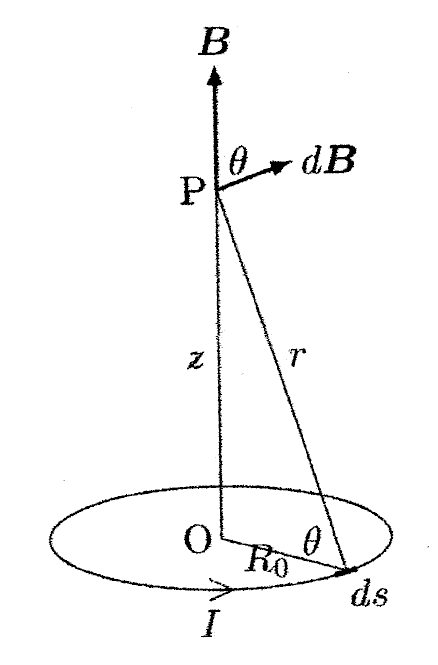
図 2
参考文献
- 1. グリフィス: 「電磁気学 I」、満田節生 他訳(丸善出版)
- 2. ゴールドスタイン:「古典力学」、野間進・瀬川富士訳(吉岡書店)
2025年11月