「重力再生エネルギー研究所」では、重力蓄電の方法以外にもいろいろな数理科学関係の研究をしています。分野の異なる話題をとり上げて、その記事をここに集めて発表します。
感染症流行の数学モデル
武笠敏夫
感染症が流行していく過程を一つの力学現象として捉え、数学的に分析できるようになったのは最近のことのようです。初期の人口モデルを始めとして、これに近代の力学系モデルを合わせて、感染症の流行モデルがつくれます。これを紹介して、またそれを分析することによってどんなことが云えるかを述べます。現象を理解するには、その現象を記述するモデルをつくります。それによって、現象を支配する定数（パラメーター）が分かり、時間発展していくメカニズムが理解されます。感染症の流行という現象を理解するために、これを行なってみます。
1.感染症の流行モデル
ある社会集団を考え、その中で感染症が拡がっていく様子を調べます。ただし、この集団は外部から独立していて、個人による外界との出入りはないとします。また、この流行は年齢構造にも依存しないと仮定します。
この集団の人口を \(n\) とし、時刻 \(t\) においてこの集団を3つのグループに分け、それぞれの人数を \(x,\ y\ ,z\) \((x+y+z=n)\) とします。ここで、\(x\) は未感染者の人口で \(y\) は感染者人口、\(z\) は除去された者（孤立者ともいう）の人口とします。とくに、この \(z\) は過去の感染により免疫を得た者や現在隔離されている者、および死亡した者の総数とします。これらの量は時間 \(t\) の関数になり、\(x=x(t),\) \(y=y(t),\) \(z=z(t)\) はつぎの連立方程式系を満 たすと仮定されます。
\begin{eqnarray} \tag{1.1} \frac{dx}{dt}&=&-\beta xy \\[0.5em] \tag{1.2} \frac{dy}{dt}&=&\beta xy-\gamma y \\[0.5em] \tag{1.3} \frac{dz}{dt}&=&\gamma y \end{eqnarray}ここで \((1.1)\) 式は、正常な者が感染症にかかって減少していく割合 \(dx/dt\) が \(x\) と \(y\) に比例することを意味します。この比例定数 \(\beta\gt0\) を感染率といいます。一方、感染者数 \(y\) の増加率 \(dy/dt\) は新しく感染して \(y\) を増加させる分 \(\beta xy\) と、既に感染した者のうち免疫ができたために \(y\) から除外される分 \(-\gamma y(\lt0)\) できまります。これを記述したものが \((1.2)\) 式と \((1.3)\) 式で、定数 \(\gamma\) は除去率といわれます。集団を構成している個人の動きとしては、初め \(x\) に属していた者が感染して \(y\) グループに移り、さらに免疫あるいは隔離によって \(z\) グループに移動することになります。したがって、連立方程式系 \((1.1)\) - \((1.3)\) はマッケンドリックの \(x-y-z\) モデルと呼ばれています。
2.感染症蔓延の条件
この現象の初期の状態を、\(t=0\) として \(x(0) = x_0,\ \) \(y(0) = y_0,\ \) \(z(0) = z_0\) とおきます。このとき、\(x_0\) はほとんど総人口 \(n\) と考えられます\((x_0\approx n)\)。すると、式 \((1.2)\) より \[ \frac {dy}{dt}\Biggl| _{t=0} = \beta y_0\biggl(x_0 - \frac{\gamma}{\beta}\biggl) \] であるから、\(\rho=\gamma/\beta\) とおいたとき、\(x_0\lt\rho\) ならば \(y\) は初めから減少していきます。すなわち、感染症は発生してもすぐに消滅してしまいます。しかし、\(x_0\gt\rho\) のときは \(y\) は増加傾向となり、これは感染症が蔓延していくことを表しています。すなわち、 \[ \tag{2.1} x_0\gt\rho \] これが感染症が蔓延する条件となります。
ところで、\(x \approx n\) であることを考慮すれば、\(x_0\) はふつう大きな数で条件 \((2.1)\) は容易に満たされていると思われます。ここで、右辺 \(\rho\) の大きさを調べてみます。一般に感染率 \(\beta\) は次のようにきまります。
\[ \tag{2.2} \beta = \frac {c\phi}{n} \]ここで、\(c\) は接触率（接触回数）で、\(\phi\) は感染確率（1回の接触によって感染が起こる確率）で表されます。したがって、定数 \(\rho\) は \[ \tag{2.3} \rho = \frac {\gamma}{\beta} = \frac {n\gamma}{c\phi} \] とかけます。\(\beta\) は人間の努力によって小さく抑えられます。また、\(\gamma\) も大きくすることは可能です。したがって、\(\rho\) は大きな値として外部から制御できる量となります。
3. 伝染病曲線
感染症が蔓延したとき、その感染者数の時間的推移を調べてみます。式 \((1.1)\) と式 \((1.2)\) から、次式が得られます。
\[ \tag{3.1} \frac{dy}{dx} = \frac{dy/dt}{dx/dt} = \frac{\beta xy - \gamma y}{-\beta xy} = -1 + \frac {\rho}{x} \]これを積分すると、軌道といわれる \(t\) をパラメーターとした曲線が得られます。すなわち、 \[ \tag{3.2} y = -(x-x_0) + \rho \log \frac {x}{x_0} + y_0 \] となります。この曲線を \(x,y\) 平面に描いたものを、図1(a)に示しました。これを基にして、関数 \(y=y(t)\) のグラフの概形が描けます（図1(b)）。
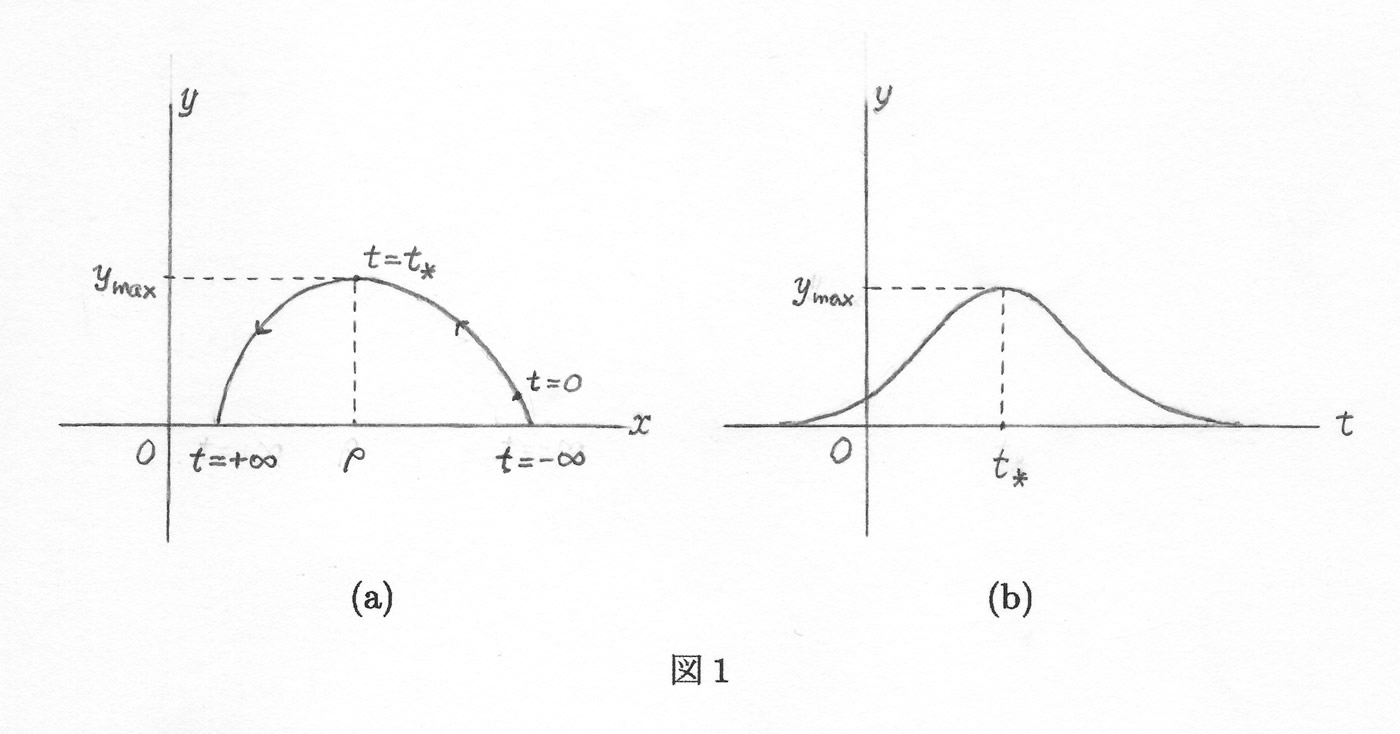
この感染者数の変化を表す曲線 \(y = y(t)\) は伝染病曲線といわれ、古くから知られてい ました。この曲線が一つのピークをもつ山型の曲線となる理由は、つぎのようにも説明 できます。式 \((1.1)\) より \(dx/dt \lt 0\) だから、\(x = x(t)\) は減少関数となります。また、式 \((1.2)\) をつぎの形で考えます。
\[ \tag{3.3} \frac{dy}{dt} = \beta y (x-\rho) \]関数 \(x = x(t)\) は蔓延条件 \((2.1)\) を満たす \(x_0\) で始まりますが、いずれ \(x \lt \rho\) となる時期が来ます（図2を参照）。いま \(x = \rho \) となる時刻を\(t = t_\ast\) とすると、式 \((3.3)\) から
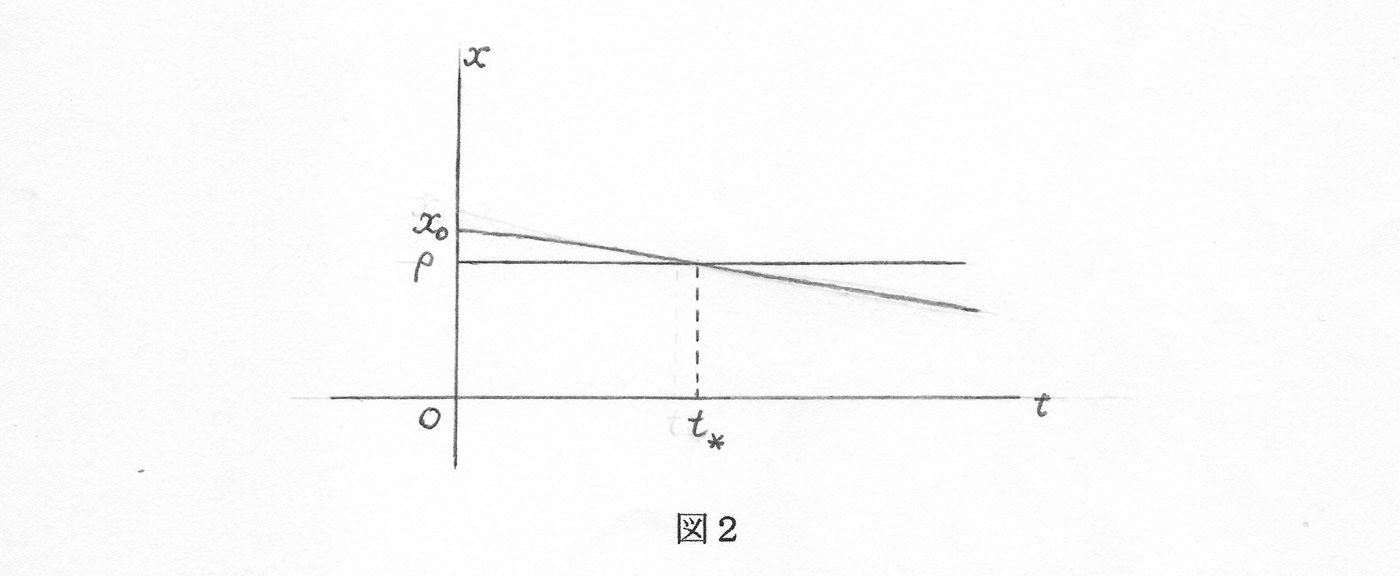\(dy/dt \lt 0\ (t \gt t_\ast)\)となります。このとき、\(y\) は減少に転じます。このピークの時刻 \(t_\ast\) が早く来るようにしたければ、\(\rho (\lt x_0)\) の値を大きくしておけばよいのです。これは、感染症が終息する時期にも関わってきます。
4.終息条件
感染症は蔓延しても、必ず終息する時が来ます。この事実を数学的に証明します。式 \((1.1)\) と式 \((1.3)\) より \(dx/dz = -(1/\rho)x\) となるから、これを解いて \(x=x_0 e^{-(z/\rho)}\) が得られます。このとき、\(y\) は \[ \tag{4.1} y=n-z-x_0 e^{-(z/\rho)} \approx n-x_0+\Big(\frac{x_0}{\rho}-1\Big)z - \frac{x_0}{2\rho^2}z^2 \] と近似できます。これを式 \((1.3)\) の右辺に代入して、 \[ \tag{4.2} \frac {dz}{dt} = \gamma \biggl( n-x_0+\Big(\frac{x_0}{\rho}-1\Big)z - \frac{x_0}{2\rho^2}z^2\biggl) \] が導かれます。終息するときの状況として \(dz/dt = 0\)（終息条件）を仮定すれば、\((4.2)\) 式の右辺で \(x_0 \approx n \) として \[ \tag{4.3} z_\infty = \displaystyle \lim_{ t \to \infty } z(t) = 2\rho \big( 1 - \frac {\rho}{x_0} \big) \] が得られます。条件 \((2.1)\) より \( x_0 = \rho + \nu \) とおいて \( \nu \gt 0 \) と仮定します。\(\rho\) の値が大きいとき、\(\nu\) は小さくなります。このとき、式 \((4.3)\) は \[ \tag{4.4} z_\infty = \frac {2\rho\nu}{\rho+\nu} \approx 2\nu \] となります。すると、\(x=n-y-z\) は \( t \to \infty \) の結果として \(x=n-2\nu\) に近づきます。\( x_0 \approx n \) に注意すれば、これは \(x\) の値が \[ \tag{4.5} x_0 = \rho + \nu \longrightarrow x_0 - 2\nu = \rho - \nu \quad (t \to \infty) \] となることを意味します。したがって、最終的に \(x \lt \rho\) が得られます。このとき、式 \((3.3)\) を用いれば、\(y\) が減少していくのが分かります。
方程式 \((4.2)\) を解くことによって、\(y = y(t)\) の関数形を具体的に知ることもできます。実際、これを実行すると \[ \tag{4.6} y = \frac{\alpha^2 \rho^2}{2x_0}\text{sech}^2\big( \frac{\alpha\gamma}{2}t-\theta \big) \] となり、ごのグラフが図1(b)の曲線を表します。ここで、\(\alpha\) は \[ \tag{4.7} \alpha = \text{tanh} \frac{x_0-\rho}{\gamma\rho} \] できまる定数であって、\(\theta\) は \(t=0\) とおいたときの \(y_0\) できまります。式 \((4.6)\) を用いると、\(y\) の最大値 \(y_\max\) についての評価がつぎのようにできます。すなわち、\(t_\ast=2\theta/(\alpha\gamma)\) で \(y\) は最大値 \[ \tag{4.8} y_\max = \frac{\alpha^2 \rho^2}{2x_0} \] をとります。もし除去率 \(\gamma\) を大きくとれば、\(\gamma\rho = \gamma^2/\beta\) は大きくなり、式 \((4.7)\) から \(\alpha\) は小さくとれます。このとき、\(y_\max\) を小さくすることができます。
5.結論
この \(x-y-z\) モデルによると、未感染者人口 \(x\) は時間と共に減少するが、そのうち感染者の中で除去される者 \(z\) が多くなり、結果として感染者人口 \(y\) は減っていくと説明されます。この理論を認めた上で、感染症が流行したとき、我々人間が為すべき対応策を考えるときに参考となるヒントをこれから導きたいと思います。
対処方法に関して問題となるのは、主につぎの2点だと思われます。
① 感染者数 \(y\) のピークの値 \(y_\max\) を低く抑えるには、どうしたらよいか。
② 流行を早く終息させるには、どうしたらいか。
課題①については、前節で述べたとおり、除去率 \(\gamma\) を上げればよいのです。この \(\gamma\) は免疫、あるいは感染者の隔離の仕方によってきまる値なので、これを大きくするためにつぎの方法が考えられます。免疫は感染者に自然に備わるものなので、外部からは制御できません。一方、感染者を隔離することは可能です。ところで、強制的に外部から免疫を持たせることはできます。これがワクチン接種の方法なのです。これは健常者 \(x\) を、\(y\) を経ずに、直接除去者グループ \(z\) に移動させることになります。
課題②に対する方策は、\(y\) 曲線のピークとなる時刻 \(t_\ast\) が早く訪れるようにします。それには、定数 \(\rho\) を大きくとって \(t_\ast\) を \(t\) 軸の左方にずらします（図2参照）。そのために、式 \((2.3)\) によって \(\gamma\) を大きく \(\beta\) を小さくすればよいのですが、とくに感染率 \(\beta\) は接触率によってきまるので、人どうしの接触を極力控えるとよいのです。
結局、一度流行してしまった感染症を抑え込むには、つぎの方法しかないようです。まず、未感染者と思われる集団の中から感染者を早急に選び出し、免疫を持つまで何らかの方法で隔離するのがよいと思われます。感染者と非感染者を混在させておくのは、\(\beta\) の値を大きくさせるだけで、大変危険なのです。
参考にした資料
1.イアネリ, 稲葉, 国谷,「人口と感染症の数理」, 東京大学出版会（2014）
2.近藤次郎,「社会科学のための数学入門」, 東洋経済新報社（1973）
6.コンピューター実験（付録）
微分方程式系 \((1.1)\) - \((1.3)\) をコンピューターを用いて解き、各集団の人口数 \(x,\ y,\ z\) の時間的推移を調べてみます。そのために、時間 \(t\) 軸を微小な区間幅 \(\Delta t (= 1/N)\) に分割し、その各格子点上だけで計算します。
以下の計算で用いた各定数の設定値はすべて共通で、\(N=1000\), \(\beta=1\), \(\gamma=100\) にとり、初期値は \(x_0=1000,\ y_0=1,\ z_0=0\) としました。
（1）感染者人口の推移：\(y= y(t)\) の時間\(t\) に対する変化を、図3(a)に示しました。また、図3(b)で \(y\) の変化率 \(dy/dt\) を描きました。これは日々の \(y\) の増分と考えられます。
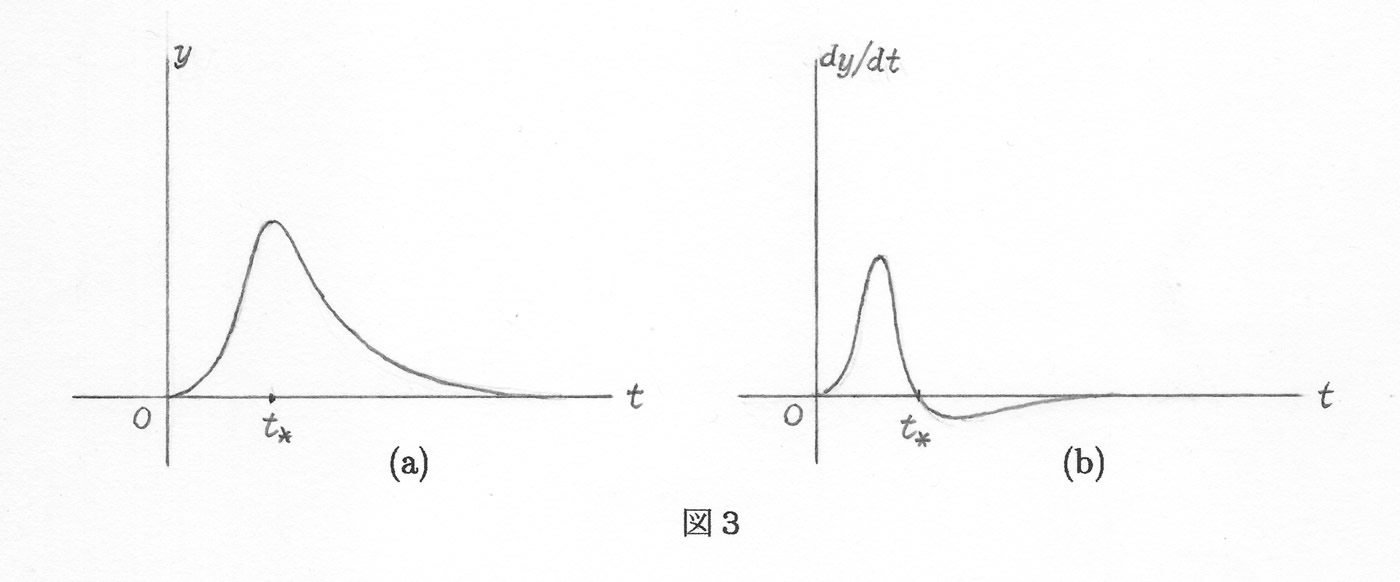
図3(b)で、この曲線がいずれ \(dy/dt \lt 0\) の領域に入る要因は、時間が経つと除去の効果が目立ってくるからです。
（2）未感染者と除去者の人口推移： 図4(a)で \(x=x(t)\) の時間変化を、また図4(b)で \(z=z(t)\) の推移を示しました。いずれも単調な曲線となります。
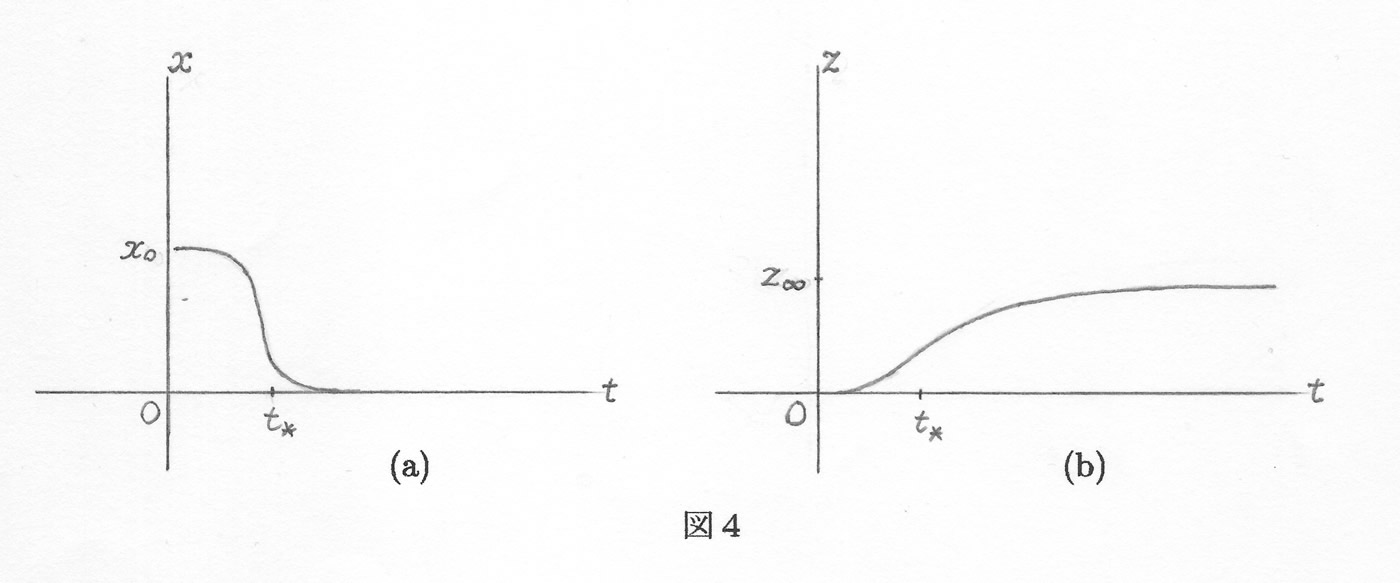
図4(a)において、未感染者人口 \(x=x(t)\) がいずれ \(0\) に近づくことが見られます。これは集団のほとんどが感染していく状況を表していますが、代わりに図4(b)では、除去者人口 \(z=z(t)\) が一定値 \(z_\infty\) に近づいていきます。すなわち、ほとんど全員が免疫を持ってくるので、これで流行は終息するものと思われます。
2020年3月
感染症流行の数学モデル2
混合型モデルとそのコンピューター実験
武笠敏夫
感染症の流行モデルを考えるとき、その特性によって感染症は大きく2種類の型に分けられます。一つは風邪や一般のインフルエンザなど何度でも感染するもので、これは主に自己免疫力だけで回復できる感染症です。もう一つは、はしかや風疹など回復する際に抗体をつくる型のものです。抗体ができるまで隔離が必要となる感染症は後者の型に分類されます。前者の型の感染症をモデル化したものは S-I-S モデルといい、後者のものを S-I-R モデルと呼びます。
感染症の中には、両方の特性をもったものも考えられます。以下では、この様な型の感染症、すなわち混合型 (S-I-S-R) モデルについて考察します。
1.基本方程式系
総人口が \(n\) の集団を考え、これを3つのグループ S, I, R に分けます。始めのグループ S (susceptible) はまだ感染していなく、免疫（抗体）がない人の集団です。グループ I (infected) は、現在その感染症にかかっている人で、R (recovered) は過去にかかったことがあり、その抗体を持っている人のグループです。現在、隔離中の者はいずれ抗体を持つと思われるので R の中に含めます。
各グループの人数は時間と共に変化します。時刻 \(t\) における S, I, R それぞれの人数を \(x = x(t),\ y = y(t),\ z = z(t)\) とします。これらの量は、\(t\) の関数としてつぎの方程式系を満たすと仮定されます。
\begin{eqnarray} \tag{1.1} \frac{dx}{dt}&=&-\beta xy+\delta y \\[0.5em] \tag{1.2} \frac{dy}{dt}&=&\beta xy-(\gamma + \delta) y \\[0.5em] \tag{1.3} \frac{dz}{dt}&=&\gamma y \end{eqnarray}ここで、\(\beta\) を感染率、\(\gamma\) を免疫率、\(\delta\) を回復率といいます。\(\gamma = 0\) のとき方程式系 (1.1) - (1.3) は S-I-S モデルを表し、一方 \(\delta = 0\) ではこの方程式系は S-I-R モデルを記述することになります。\(\gamma \gt 0\), \(\delta \gt 0\) のときは両方の要素を持つことになり、S-I-S-R モデルあるいは混合型といわれます。混合型では、感染者は回復して抗体をつくる場合と、自己免疫力で回復しても抗体をつくらない場合があることに注意します。
2.S-I-S モデル
この型の感染症の流行では、S の中の未感染者は感染して I 集団に移るのですが、自己免疫力によって回復すると抗体をつくることなしに再び S 集団に戻るという S と I の間の行き来が起き、複数回の感染が生じることもあります。この感染症は、回復しても抗体をつくらないのです。
このモデルは、式 (1.1) と式 (1.2) で \(\gamma = 0\) とおいた方程式系によって記述されます。このとき、総人口 \(n=x+y\) を考慮すると、(1.2) 式より \[ \tag{2.1} \frac{dy}{dt}=\beta(n-y)y-\delta y=(\beta n - \delta)y-\beta y^2=\lambda_0y-\beta y^2 \] が得られます（\(\lambda_0=\beta n-\delta\) とおいた）。方程式 (2.1) を解くと、解は \[ \tag{2.2} y = \frac{y_0 e^{\lambda_0 t}}{1+(\beta/\lambda_0)(e^{\lambda_0 t}-1)} ,\quad y(0)=y_0 \] となります。一般に \(n\) は大きな数なので、\(\lambda_0 \gt 0\) と考えられます。すると、(2.2) 式で \(t\rightarrow\infty\) とすれば \(y\rightarrow(n-\sigma)y_0\) \((\sigma=\delta/\beta)\) となります。すなわち、このモデルでは感染症は決して終息することはありません。
3.混合型モデル
方程式系 (1.1) - (1.3) において、ベクトル場すなわち右辺のつくる様相がパラメーター \(\gamma\) の動きによってどのように変化するか、を調べてみます。
式 (1.1) と式 (1.2) より、次式が得られます。
\[ \tag{3.1} \frac{dy}{dx}=\frac{\beta xy-(\gamma+\delta)y}{-\beta xy+\delta y}=-1+\frac{\gamma}{\beta x-\delta}=-1+\frac{\rho}{x-\sigma} \]ここで、\(\rho=\gamma/\beta\), \(\sigma=\delta/\beta\) とおきました。これを積分すると、解は \[ \tag{3.2} y=-x+\rho \log|x - \sigma|+C \] この式の中で積分定数 \(C\) は、初期値 \(x(0)=x_0\), \(y(0)=y_0\) を用いて、\(y_0=-x_0 +\rho \log|x_0 - \sigma|+C\) より決まります。\(\beta\) を固定して、\(\gamma\) を \(0\) から徐々に増やしていきます。したがって、式 (3.2) で \(\rho=0\) より \(\rho \gt 0\) と変化させます。これによって、ベクトル場が S-I-S モデルから S-I-S-R モデル、すなわち混合型へ変位していく様子が見てとれます（図1(a),(b)参照）。
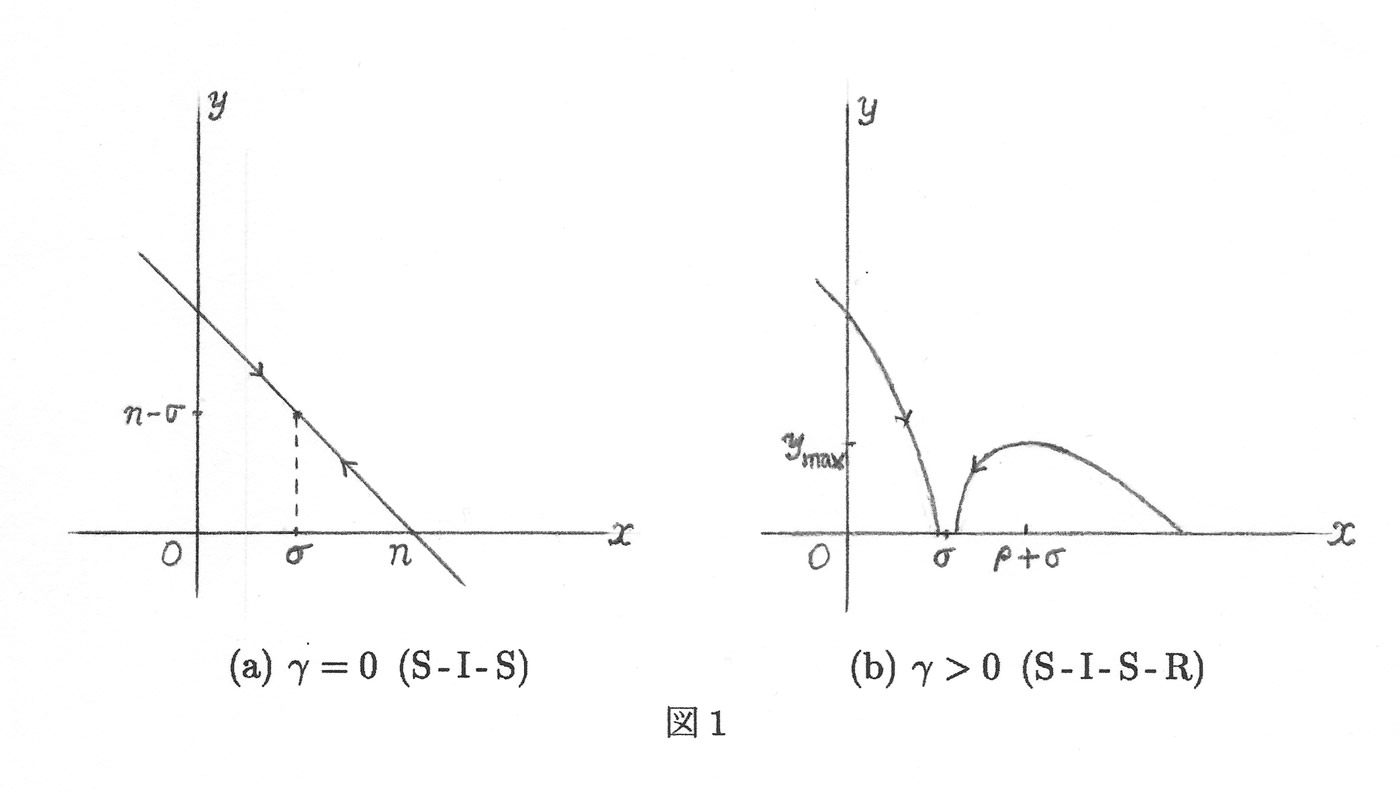
これによると、始め小さい \(y=y_0\) から出発した軌道は、\(\gamma=0\) のとき \(y= y(t)\) が単調に増加して \(y=n-\sigma\) に収束するのに対して、\(\gamma \gt 0\) では \(y\) が一度極大となってゆっくりと \(y=0\) に収束していくのが分かります。このときのピークの値 \(y_\max\) はつぎのように計算されす。\(x=\rho+\sigma\) のときの \(y\) の値として \[ \tag{3.3} y_\max = \rho \left( \log \frac{\rho}{x_0 - \sigma} -1\right)+n-\sigma \] ときまります。このときの、関数 \(y= y(t)\) のグラフの形状は次節で調ベます。
4.コンピューター実験
S-I-S-R モデル（混合型）が S-I-R モデルと比較してどこが異なるのか、を考察します。すなわち、方程式系 (1.1) - (1.3) において、\(\delta\) の項がこの現象にどのような効果を及ぼすかを調べてみます。そのために、この方程式系を差分法で近似して、\(\delta =0\) の場合と \(\delta \gt 0 \) の場合とに分けて両者の解を比較します。
時間 \(t\) 軸を長さ \(\varDelta t = 1/N\) の微小区間に分け、その端点のつくる格子点上だけで考えます。格子点に番号を付け、時刻 \(t=i\varDelta t\) における \(x(t),\ y(t),\ z(t)\) の値を \(U(i),\ V(i),\ W(i)\)で表します。そこで、方程式系 (1.1) - (1.3) を差分化すると、 \begin{eqnarray} \tag{4.1} U(i+1) &=& U(i)+(\varDelta t)(-\beta U(i)V(i)+\delta V(i)) \\[0.5em] \tag{4.2} V(i+1) &=& V(i)+(\varDelta t)(\beta U(i)V(i)-(\gamma + \delta)V(i)) \\[0.5em] \tag{4.3} W(i+1) &=& W(i)+(\varDelta t) \gamma V(i) \end{eqnarray} となります。以下の計算では、\(\varDelta t = 1/1000\) で \(\beta = 1,\ \gamma = 100\) にとり、\(\delta\) の影響が強調 されるように、\(\delta = 0\) と \(\delta = 500\) にとってその解を比べてみます。結果はつぎのようになりました。
（1）感染者数 \(y = y(t)\) :
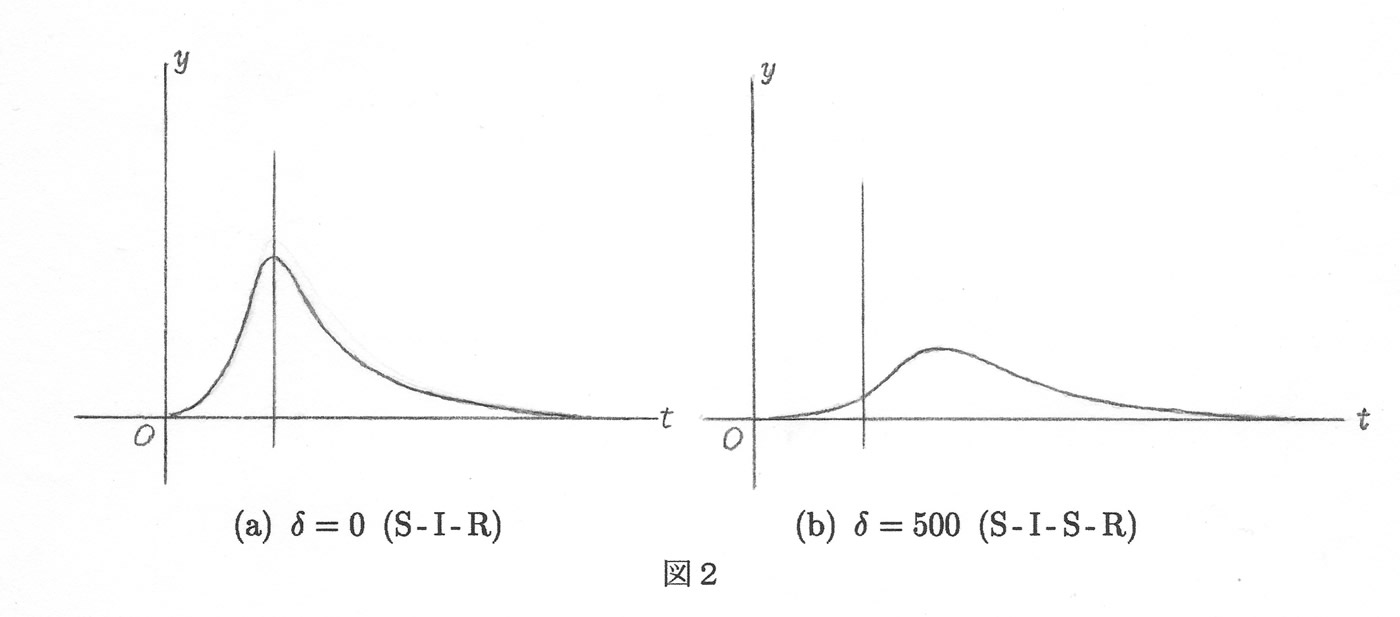
これによると、S-I-S-R モデル（混合型）は、S-I-R モデルの場合に比べてピークの訪れる時期が遅れ、しかもピークの高さも低くなる傾向があるようです。これは、抗体をつくって回復する場合と自己免疫力による回復があり、また複数回感染する場合があるためと思われます。したがって、混合型は終息しにくいという特徴が見られます。
（2）未感染者数 \(x=x(t)\) :
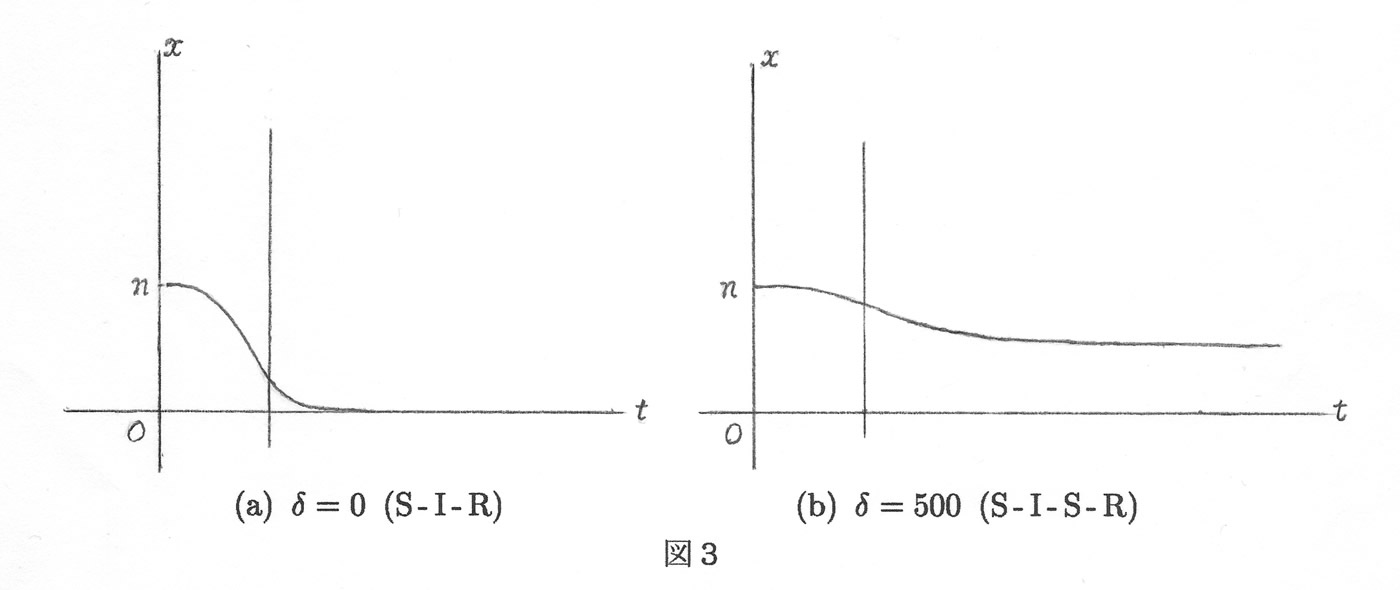
混合型では、未感染者は終息後も一定の割合で存在するのですが、この中には全く感染しなかったか、または感染しても抗体なしで回復した人が含まれます。これは自己免疫力によるものと思われます。
（3）抗体保持者数 \(z= z(t)\) :
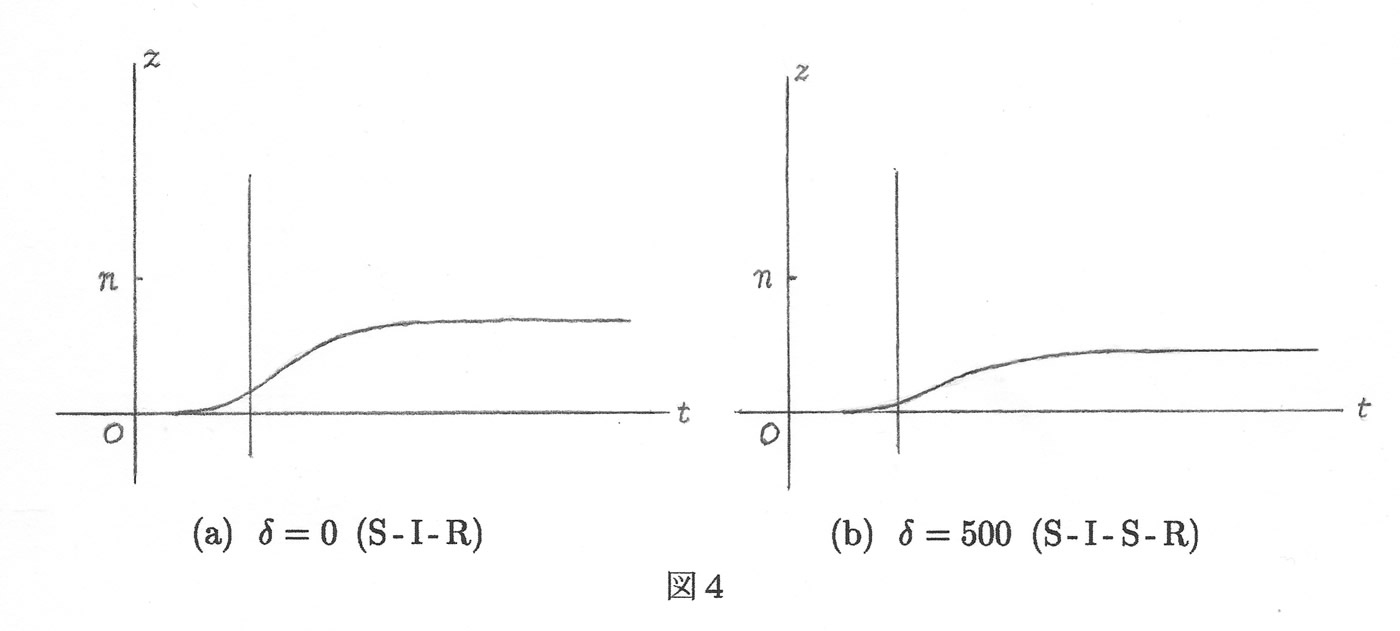
これは興味深い結果だと思われます。すなわち、S-I-R モデルでは終息するまでに抗体保持者が人口全体の 70% 程度必要であるのに対して、混合型では約 40% でよいという結果が見てとれます。
5.結論
混合型（S-I-S-R）モデルの大きな特徴の一つは、感染者は抗体を持たなくても自己免疫力だけで回復できるということです。一般に、若い年齢層（特に子供）は自己免疫力が強くこの感染症にかからないか、たとえ感染しても直ちに回復してしまうという現象が、この混合型によって説明できます。この場合、抗体によらないので過去に感染したことがあるという痕跡は残りません。
さらに重要なのは、その集団の中で抗体を持つ者が 50% 未満でもこの感染症は終息が可能な点です（図4(b)参照）。抗体の数だけが終息を決めることにはならないのです。これは抗体を持たずに回復する者が多数いるからです。
一方で、自己免疫力で回復した者の中には再び感染する者も出て来ます。したがって、この感染症は大きな感染爆発もない代わりに終息しにくいという特徴があります（図2(b)参照）。これはやっかいな疫病と云えます。
2020年5月