1. 大規模蓄電の必要性
再生可能エネルギーの利用に伴って、大量に電力を溜める技術は必ず必要となります。それは、この発電方法が気象条件などに左右され、供給に不安定さがあるためです。また、工業用などエネルギーを大量に消費する場合は、それを大規模に貯蔵して使用する必要があります。
現在電気を溜める方法は、実用化されているもので二つの方法しか人間は持っていません。一つは化学反応ポテンシャルを使用する蓄電池(バッテリー)で、もう一つは力学ポテンシャルを利用した揚水発電だけです。蓄電池は利便性に優れているが故に大きな進歩を遂げてきたのですが、大量貯蔵には向いていません。一方、揚水発電は大規模蓄電には適していますが、ダムを必要とします。
つぎの時代に備えて、別の蓄電技術を開発しておくべきです。容易に思いつくのは、揚水発電を進化させて、重力ポテンシャルを利用した重力蓄電の方法です。これはダムを必要としません。以下に、この重力を利用した大規模蓄電のシステムについて説明します。
2. システムの概容
出来るだけ高さのある塔(タワー)を建てます。このタワー一基に占める土地の面積は 2 メートル四方もあれば十分です。横揺れに対する補強よりも、縦方向の構造だけは強固につくる必要があります。タワーの内部には、重りが滑らかに通過できるようにガイドを設置しておきます。上部にある電動機を用いて、外部電力により重りをタワーの上部まで吊り上げておきます。これで、与えられた電力が重力に対する位置エネルギーの形で蓄えられたことになります。これはバッテリーで云えば充電です。一方、重りの落下により上部の電動機を発電機として回転させれば、電力が生成されます。これで重りに蓄えられた位置エネルギーが電気エネルギーとして放出されたことになり、放電に相当します。
このように装備されたタワーは、一基だけでは蓄電システムとしての機能はありません。実用に供するには、このタワーを数 100 基から数 1000 基ほど用意して、これらのいくつかを同時にあるいは連続的につぎつぎと運転できるようにします。それによって出力の時間および出力電力を調整することが出来ます。このタワーの構造は単純でコンパクトに設計されているので、これらの集合体をつくることが容易となり、多くの機能を持たせることができるのです。
具体的には、100 (m) × 100 (m) 程度の広さをもつ建物の中に、このタワーを束にして格納します。タワーを半地下に設置すれば、建物の高さを低く抑えることができます。タワー一基の占める面積が小さいので、50 基 × 50 基 ほど設置することが可能となります。
タワー一基の出力が小さくても、そのいくつかを同時に並列運転すれば出力は可算されます。また、複数個のタワーを順番に直列運転すれば、稼働時間を倍増させることができます。もちろん、これらは自動で制御されます。
重りとしては密度の高い金属を使用すればよいのですが、鉄ならば 1 立方メートルで約 8 トンとなります。したがって、タワー一基につき数 10 トンの重りを装備することは可能です。この重りをギアの組み合わせによって適切な速度で落下させれば、出力と時間を制御することができます。
3. 出力試算
タワー一基の出力はつぎのように計算されます。重りに蓄えられるポテンシャルエネルギー(位置エネルギー)は、重りの重量とタワーの高さに比例します。いま、高さ \(l = 100\ \mathrm{(m)}\)、重量 \(m = 30\ \mathrm{(ton)}\) とするとき、位置エネルギー \(U\) は \[ \tag{3.1} U = mgl = 30 \times 10^{3} \times 9.8 \times 100 = 2.94 \times 10^{7}\ \mathrm{(J)} \] となります。ここで、比例定数 \(g = 9.8\ \mathrm{ (m/sec^{2})}\) は重力加速度といいます。エネルギー(仕事)の単位はジュール \(\mathrm{(J)}\) が使われます。もし、これを 30 分かけて落下させたとき、これがすべて電気エネルギーとして出力されるとすれば、その電力を仕事率 \(P\) (単位をワット \(W = \mathrm{J/sec}\))と見なして、 \[ \tag{3.2} P = mgl/t_0 = 2.94 \times 10^{7}/(30 \times 60) = 16.33\ \mathrm{(kW)} \] の電力が得られます。これはタワー一基あたりの瞬間出力ですが、落下時間 \(t_0\) を長くすれば電力としての出力は小さくなります。
つぎに、このタワーを \(100\ \mathrm{(m)} \times 100\ \mathrm{(m)}\) の広さの建物に 2500 基まとめて収納すると、これらに蓄えられるエネルギーの総量は
\[ \tag{3.3} 2.94 \times 10^{7} \times 2500 = 7.35 \times 10^{10} \mathrm{(J)} \] となります。\(1\ \mathrm{(kWh)} = 3.6 \times 10^{6} \mathrm{(J)} \) なので、このエネルギーは \(20.4\ \mathrm{(MWh)}\) の電力量に相当します。さらに、この規模の建物を 10 棟分設置すると総出力 \(204\ \mathrm{(MWh)}\) の蓄電プラントがつくれます。揚水発電に必要なダムの面積は数 10 ヘクタール( 1 ヘクタール = 100 (m) × 100 (m))であって、この重力蓄電プラントの 10 棟分に要する土地面積はダムに比べれば少なくて済むのです。とくに、山地のない地方や国々でダムがつくれないところでは、この蓄電システムは大いに有効となると思われます。
以上の試算は全く理論的なもので、途中のエネルギー損失や効率は一切考えていません。実際には、この試算で示した数値の半分も実現できればよいと思います。しかし、これら効率を上げることは将来の技術力に委ねます。
4. 構想図

半地下の建物の中に多くのタワーが収納されている。
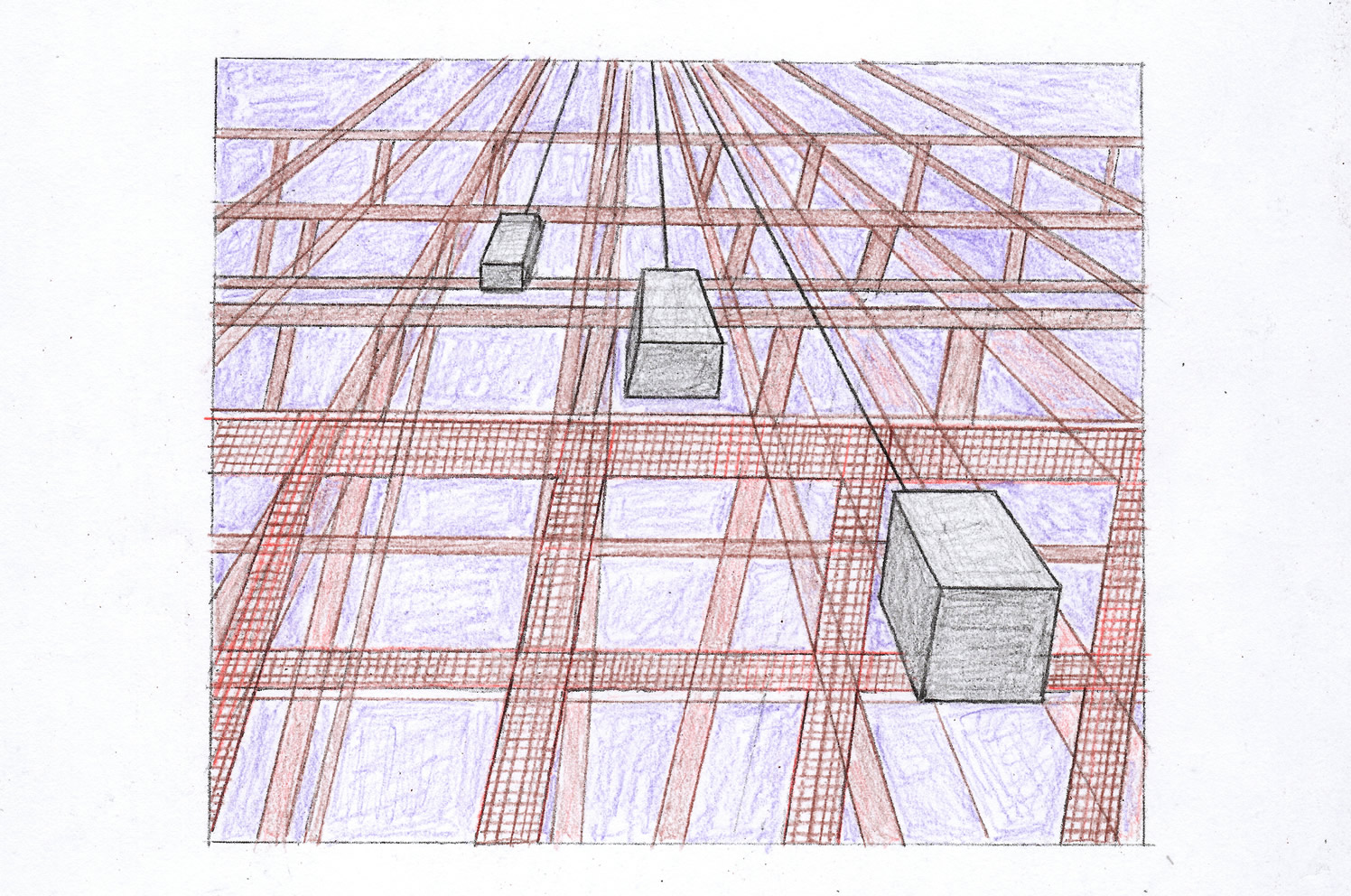
たくさんのタワーの束を下から見上げている。
2021年4月
家庭用重力蓄電は可能か?
(小規模重力蓄電システムの設計)
太陽光発電によって得られた電力のうち、昼間使って余った電力を重力を利用して蓄電することを考えます。もしこれが家庭でできるようになれば、環境に優しい持続可能な個別のエネルギー体系が出来あがります。
そこで、これを実現するために、家庭用として設置可能な小規模重力蓄電システムの設計をしてみます。装置として必要な規模を決めるために、以下の条件のもとでのエネルギー試算をしてみます。
条件:
1.装置を設置するに十分な敷地面積が確保できるとする。
2.タワーの高さは、最高 \(10\ \mathrm{(m)}\) 以下とする。
3.電力使用量は1日あたり \(10\ \mathrm{(kWh)}\) とする。
4.計算上、エネルギー損失は考慮しない。
1. 電力と電力量
エネルギーとしての電力量を考えるとき、電力との関係については十分な注意が必要です。エネルギーの単位は仕事と同じで、\(\mathrm{(J)}\) ジュールで測ります。単位時間あたりの仕事をする割合を仕事率といい、\(\mathrm{(J/s) = (W)}\) ワットで表します。電気の場合では、これが電力に相当します。したがって \(\mathrm{(J) = (Ws)}\) となり、これを電力量といって電気的エネルギーを表します。\(1\ \mathrm{(kW)}\) の電力で \(1\ \mathrm{h}\) \(\mathrm{(}\)時間\(\mathrm{)}\)にする仕事\(\mathrm{(}\)電力量\(\mathrm{)}\)を \(1\ \mathrm{(kWh)}\) とかきます。
公式:電力量について、\(1\ \mathrm{(kWh)} = 3.6 \times 10^{6}\ \mathrm{(J)}\) が成り立つ。
実際、\(1\ \mathrm{(h)} = 3600\ \mathrm{(s)}\) だから、 \[ 1\ \mathrm{(kWh)} = 10^{3}\ \mathrm{(W)} \times 1\ \mathrm{(h)} = 10^{3}\ \mathrm{(J/s)} \times 3600\ \mathrm{(s)} = 3.6 \times 10^{6}\ \mathrm{(J)} \] となります。
2. 基本的な試算
上の条件のもとで、重力蓄電に要する設備の規模を算出してみます。一日あたりの電力使用量 \(10\ \mathrm{(kWh)}\) をすべて重力蓄電\(\mathrm{(}\)位置エネルギー\(\mathrm{)}\)で賄うものとします。重りとして \(4^{3}\ \mathrm{(m^{3})}\) の鉄を使用すると、鉄 \(1\ \mathrm{(m^{3})}\) の重りが \(7.9\ \mathrm{(ton)}\) だから、この重りの重量は \(m = 7.9 \times 4^{3} = 506\ \mathrm{(ton)}\) となります。この重りに蓄えられる位置エネルギー \(U\) が \(10\ \mathrm{(kWh)} = 3.6 \times 10^{7}\ \mathrm{(J)} \) となるに必要な高さ \(\it{h}\) は、\(U = mgh = 506 \times 10^{3} \times 9.8h = 3.6 \times 10^{7}\) より求められます。実際、\(h = 7.2\ \mathrm{(m)}\) が得られます。これなら建物1棟の中に装置を収納できる大きさとなります。ただし、このままでは重りのサイズが大きいので、これを分散させる工夫が必要です。
実際には、太陽光で発電するにしても、使用する電力のすべてを一度蓄電したものから改めて消費することは殆んどあり得ないので、使用量の一部を蓄電によって賄えばよいと思われます。したがって、考えられる蓄電装置はここで述べたもの程大きくする必要はなくなります。
3. 太陽光発電
ソーラーパネル1枚の定格出力が \(230\ \mathrm{(W)}\) のものを使用します。これは瞬間出力であって、\(\mathrm{W} = \mathrm{J/s} \) を考慮すれば、1時間では \(230 \times 3600 = 828000\ \mathrm{(J)} \) の発電をすると解釈されます。すると、電力量の公式より、これは \(828000/(3.6 \times 10^{6}) = 0.23\ \mathrm{(kWh)} \) の電力量に相当します。
このパネルを20枚用意したとすると、1時間あたりの総出力は \(0.23\ \mathrm{(kWh)} \times 20 = 4.6\ \mathrm{(kWh)} \) となります。1日の実稼動時間を3時間として \(4.6 \times 3 = 13.8\ \mathrm{(kWh)}\) となり、これが1日あたりの発電量といえます。ただし、これは晴天が続いた場合であって、実際の1年を通した平均値としてはこれよりかなり少なくなると思われます。
太陽光発電ですべての電力を賄うとき、蓄電に頼らなければならない理由が二つあります。それは以下の場合です。
\((1)\) 夜間の電力使用に対応する。
\((2)\) 曇天のために殆んど発電が行われない場合。
これらの対応策として、\((1)\) では昼間の発電量の一部を夜間用に蓄電しておく必要があります。\((2)\) の場合は、普段から非常用として特別に溜めておくことにします。
4. 重力による蓄電
重りとして \(1\ \mathrm{(m^{3})}\) の鉄を縦に2個並べたものを用意します。この重量は \(m = 7.9 \times 2 = 15.8\ \mathrm{(ton)} \) になります。高さが \(h = 10\ \mathrm{(m)} \) のタワーの上部に発電機を設置して、重りの落下により発電機が回転するような装置をつくります。これをタワーユニットといいます。外部からの電源により、発電機を電動機の代わりにして重りを上部に持ち上げたとき、それに蓄えられる位置エネルギーは \[ \tag{4.1} U = mgh = 15.8 \times 10^{3} \times 9.8 \times 10 = 154.84 \times 10^{4}\ \mathrm{(J)} \] となります。これを電力量に換算すると、 \[154.84 \times 10^{4} /(3.6 \times 10^{6}) = 0.43\ \mathrm{(kWh)}\] に相当します。これがユニット1基に蓄えられる電力量です。
このユニットを縦横5列づつ25基並べて、床面積が \(8\ \mathrm{(m)} \times 8\ \mathrm{(m)} = 64\ \mathrm{(m^{2})} \) の建物内に収納します。これでこの重力蓄電によって蓄えられる電力量の総量は \[ \tag{4.2} P = 154.84 \times 10^{4} \times 25/(3.6 \times 10^{4}) = 10.75\ \mathrm{(kWh)} \] になります。8メートル四方の建物の中に、高さ \(10\ \mathrm{(m)} \) のユニットを半地下にして25基並べることはそれほど難しいことではありません。稼働の仕方としては、仮に太陽光による発電量が1日あたり \(10\ \mathrm{(kWh)} \) あったとして、昼間 \(6\ \mathrm{(kWh)} \)使用して夜間用に \(4\ \mathrm{(kWh)} \) の電力を蓄電しておくなどが考えられます。この程度の装置ならば、昼間使用した残りの電力を非常用にフル蓄電しておくことも可能になります。太陽光発電は天候に大きく左右されるので、蓄電によって平滑化する必要があるのです。
5. 結論
再生可能エネルギー、とくに太陽光発電や風力発電を利用するとき、その電力を安定的に供給するには蓄電設備が必要となります。家庭用蓄電設備を考えるとき、その利便性とコンパクト性から蓄電池\(\mathrm{(}\)化学バッテリー\(\mathrm{)}\)を設置するのが普通のようです。しかし、地球環境と持続性の観点から見れば、将来的には他の蓄電方法を考えておく必要があります。
重力を利用した蓄電方法は環境に優しく、一度設置すれば半永久的に使用できます。しかしながら、同じ蓄電容量に対する設備の大きさを、蓄電池と重力蓄電について比べると、圧倒的に重力蓄電の場合の方が大掛かりとなります。蓄電池ならば小さな物置き\(\mathrm{(}\)ロッカー\(\mathrm{)}\)に収納できるのに対して、重力蓄電の設備は専用の建物を1棟建てなければなりません。この差をどのように考えるかが問題です。両者を評価するとき、単純にコストとか効率によって優劣を付けてしまってよいのかは、その時代の判断となります。地球環境のためには、再生可能エネルギーを再生可能な方法で溜めて使うのがよいと思うのですが、如何でしょうか。
ここで述べた試算は、エネルギー変換の際のエネルギー損失分を考慮せずに算出したもので、実際にはこの数値どおりにはなりません。理論的にはこれ以上の数値を期待することは不可能であるということであって、将来の技術力によって、この理論値に近づけることは可能です。
2021年9月